مکانیک کوانتومی، ساختار ماده و برهم‌کنش آن با میدان الکترومغناطیس را توصیف می‌کند. این نظریه به ما اجازه می‌دهد تا اندازه، هندسه و انرژی پیوند ساختارهای اتمی و مولکولی را محاسبه کنیم. توصیف دقیق و کمی این پارامترها نیازمند حل معادلاتی با پیچیدگی زیاد است. در این متن سعی می‌کنیم با استفاده از قوانین اصلی مکانیک کوانتومی، اثرات مهم فیزیکی دو پدیده‎‌ی بزرگ مقیاس را تخمین بزنیم.

سختی جامدات:

چرا جامدات، جامد (سخت) هستند؟ سختی یک جامد با مقاومت آن در برابر فشار سنجیده می‌شود و مدول تراکمی جامد تعریف می‌شود: C=P V/∆V که P فشار وارد بر جامد و V/∆V تغییر نسبی حجم است. می‌خواهیم مقدار آن برای یک جامد را تخمین بزنیم.
برای سادگی فرض کنید اتم‌های جامد تک ظرفیت‌اند و N یون مثبت در داخل یک گاز N الکترونی تشکیل بلور داده‌اند. هر الکترون حجم آزاد قابل دسترس V/N دارد و انرژی جنبشی آن تقریبا E_k=ℏ^2/(md^2 ) است که d=(V/N)^(1/3) فاصله‌ی بین دو یون بلور را به دست می‌دهد. هر الکترون به طور تقریبی در ناحیه‌ای به حجم d^3 محبوس شده و در نتیجه فشار ناشی از انرژی جنبشی آن تقریبا P=ℏ^2/(md^5 ) است. d معمولاً از مرتبه‎ی چند شعاع بور( a₀ ) است و اگر فرض کنیم d=4a₀=2 Å، مقدار تخمینی P~5×10^10 Pa را به دست می‌دهد. ممکن است تصور کنید چنین فشاری به وسیله‌ی الکترون‌ها باید جامد را از هم بگسلد اما جاذبه‌ی کولنی بین الکترون‌ها و یون‌ها مانع از این عمل می‌شود. در هر صورت برای تغییر حجم قابل توجه در جامد انتظار می‌رود که فشاری از این مرتبه به آن وارد کنیم و در نتیجه C از مرتبه‌ی 10^10 Pa است. این عدد با مقادیر اندازه‌گیری شده برای جامدات سازگار است.

ذوب شدن جامدات و ارتفاع کوه‌ها:

برای یک جسم نسبتاً کوچک سماوی که برهم‌کنش گرانشی به صورت قوی در آن غالب نیست، نیروی گرانشی می‌تواند تاثیر زیادی بر شکل جسم داشته ‌باشد. کوهی بر روی این جسم سماوی (سیاره یا سیارک) نمی‌تواند خیلی بلند باشد؛ در غیر این‌صورت کوه ترجیح می‌دهد با ذوب کردن پایه‌ی خود، انرژی پتانسیل گرانشی را به گرمای نهان مورد نیاز برای ذوب کردن کوه تبدیل کند.
برای ذوب کردن کسری از یک جامد متشکل ازδN اتم انرژی‌ای از مرتبه 10^(-2) E_I×δN نیاز است که E_I انرژی پیوند آن جامد است. به صورت دقیق‌تر به ازای هر اتم، کسر کوچکی (حدود 5 درصد) از انرژی پیوند نیاز است تا جامد ذوب شود.
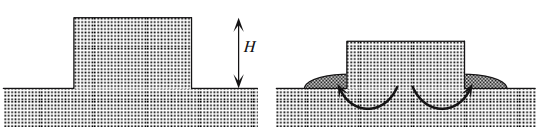
یک کوه بر روی زمین با ساختار استوانه‌ای شکل (برای سادگی) و ارتفاع H در نظر بگیرید. تغییر انرژی پتانسیل گرانشی ناشی از ذوب شدن δN اتم برابر است با: δEp=δMgH که   δM=Amp δN که A عدد جرمی هر اتم و mp جرم پروتون است. کاهش ارتفاع کوه از لحاظ انرژی برای کوه مرجح است اگر δEp کم‌تر از انرژی δE_l موردنیاز برای ذوب مقدار δM از کوه باشد. از پاراگراف قبل می‌دانیم انرژی موردنیاز برای ذوب 〖δE_l=10〗^(-2) E_I δN است، پس فرآیند ذوب شدن تا زمانی که ارتفاع کوه از مقدار H در رابطه زیر کم‌تر شود ادامه می‌یابد:
δEp≤δE_l→Amp gH≤10^(-2) E_I
برای ماده‌ی سازنده‌ زمین، A~50، E_I~ 0.2 ،Ry ~ 2.7 eV و مقدار H~27 km برای تساوی رابطه‌ی بالا به دست می‌آید. مقدار واقعی بلندترین کوه‌ها روی زمین تقریباً 10 km است که با مدل ساده شده‌ی ما سازگاری بسیار خوبی دارد. اولین بار ویکتور وایسکوف بحث بالا را درباره‌ی ارتفاع کوه‌ها بیان کرد.

شکل 1: یک کوه روی زمین می‌تواند پایدار باشد در صورتی که ارتفاع خیلی زیادی نداشته باشد. در غیر این‌صورت ترجیح می‌دهد با ذوب کردن پایه خود انرژی پتانسیل گرانشی را به گرمای نهان ذوب تبدیل کند.

منابع:
[1]J.L. Basdevant, J. Dalibard, Quantum Mechanics, Springer 2005

اگر نظر یا پیشنهادی درمورد این متن دارید می‌توانید کمی پایین‌تر، در قسمت دیدگاه‌ها، آن را برای ما بنویسید.