کتاب فلسفۀ فیزیک: فضا و زمان

تولد فیزیک

سنت فکری‌ای که فیزیک نظری مدرن را به‌وجود آورد از دوران یونان باستان آغاز می‌شود. اخترشناسان بابلی و مصری اطلاعاتی زیاد و دقیق دربارۀ موقعیت‌های مشاهده‌پذیر خورشید و سیارات تدوین کردند و مدل‌هایی ریاضیاتی به‌وجود آوردند که با آن‌ها می‌شد پدیده‌هایی مانند ماه‌گرفتگی و خورشیدگرفتگی را پیش‌بینی کرد. اما فیلسوفان طبیعت یونانی خطی جدید از نظریه‌پردازی نظرورزانه را وارد این عمل مربوط به مشاهده کردند. مثلاً طالس، آناکساگوراس و دموکریتوس هریک دربارۀ ساختار نهایی ماده نظریه‌هایی دادند: این‌که همۀ اشیاء مادی از آب نشأت گرفته‌اند، یا این‌که همه مخلوطی از خاک، هوا، آتش و آب هستند، یا این‌که اشیاء ترکیبی از کثرتی نامتناهی از اتم‌هایی هستند که اشکال متفاوت به خود گرفته‌اند. در نتیجه، رفتار قابل مشاهدۀ ابژه‌های آشنا برحسب این ساختار مادی تشریح شده بود. به عقیدۀ دموکریتوس، چیزهای شیرین از اتم‌های صاف و گرد و چیزهای ترش از اتم‌های زاویه‌دار تشکیل شده‌اند و الی آخر. این عقیده که خواص و رفتار ملموس اشیاء بزرگ را باید به‌کمک ساختار و ماهیت بخش‌های نامرئی آن‌ها تبیین کرد تا به امروز در بنیان فیزیک نهفته بوده است.

ارسطو برای این کار نظرورزانه نامی در نظر گرفت. عبارت «فیزیک» برگرفته از متنی از ارسطو به نام «فوسیکه آکرواسیس» است که به معنی درس‌گفتارهایی در باب طبیعت است. در یونان، «فوسیک» به طبیعتِ هرچیز اشاره دارد و ارسطو طبیعت یک ابژه را سرچشمۀ درونی حرکت و سکونش تعریف می‌کند که در وهلۀ اول و حقیقتاً، و نه به‌طور تصادفی، به خود آن ابژه تعلق دارد. بنابراین به عقیدۀ ارسطو طبیعتِ هر ابژه‌ای این‌گونه آشکار می‌شود که وقتی کاملاً به‌حال خود رها شده باشد، چگونه حرکت می‌کند و از حرکت باز می‌ایستد. سنگی را بدون اعمال فشار به آن در هر جهت در هوا رها کنید، سنگ به میل خود به طرف پایین حرکت می‌کند. حباب هوای داخل مخزن آب خودبه‌خود بالا می‌آید. سنگ و حباب هوا را فقط تحت تأثیر عاملی خارجی می‌توان به انجام کارهای دیگری وادار کرد. تمایلات ذاتی آن‌ها به حرکت و سکون ناشی از عوامل بیرونی نیست و بنابراین باید برخاسته از همان طبیعت خودشان باشد.

کاملاً درست و به‌جاست اگر بگوییم که سنگ به‌طور طبیعی سقوط می‌کند، یا رو به پایین حرکت می‌کند؛ اما منظور از «رو به پایین» دقیقاً چیست؟ این‌جاست که ارسطو عقاید رایج را رها می‌کند و اصول موضوعۀ نظری خود را مطرح می‌کند. طبق نظر ارسطو، حرکت رو به پایین، حرکت به طرف یک مکان خاص است. در این دیدگاه، حرکت طبیعی زمین هدفمند است. على‌الخصوص، سنگ می‌خواهد به مکانی برسد و همیشه حرکت خودبه‌خودی‌اش آن را به این هدف غایی نزدیک‌تر می‌کند. به نظر ارسطو، مکان خاصی که سنگ برای رسیدن به آن تلاش می‌کند مرکز جهان است. ارسطو می‌پنداشت که همۀ عالم مادی به شکل کره‌ای است که سطح خارجی آن شامل ستارگان ثابت است. سپهر سماوی مرکزی یگانه دارد. جهت «پایین» در هر مکانی در جهان، به سمت آن نقطۀ مرکزی است و طبیعت هر ذرۀ خاکی به گونه‌ای است که اگر مانعی وجود نداشته باشد، در یک خط راست به‌سمت مرکز پایین می‌رود تا این که به هدف برسد و اگر تمام مسیر به سمت مرکز را طی کند، آن وقت بالطبع متوقف خواهد شد.

به طور مشابه، «بالا» جهتی در فضاست که مستقیماً به دوری از مرکز اشاره دارد. آتش و هوا به‌طور طبیعی در خطوط مستقیم تا آن‌جا که بتوانند به‌سمت بالا حرکت می‌کنند و اگر رقابت کنند، آتش از هوا پیشی می‌گیرد. به عقیدۀ ارسطو، اگر عالم تحت القمر (آن بخش از جهان که زیر مدار ماه قرار دارد) کاملاً آزاد، به حال سکون رها شود، خاک، هوا، آتش و آب، همه به‌طور طبیعی به چهار کرۀ هم‌مرکز مجزا می‌شوند: خاک خالص در مرکز، به‌نوبت توسط پوسته‌های کروی هم‌مرکزی شامل آب، سپس هوا و بعد آتش محاصره می‌شود.

 

قانون اول نیوتن و فضای مطلق

قانون اول: هر جسم بر حالت خودش، سکون یا حرکت یکنواخت در یک خط راست، پایداری می‌کند مگر زمانی که تحت تأثیر نیروهایی مجبور به تغییر حالتش شود.
این قانون بی‌نظیر جهان ارسطو را ویران ساخت. اول آن‌که، قانون نیوتن بر هر جسمی، اعم از سنگ‌ها و سیارات، به یک شکل حاکم است. نیوتن تفاوت بین اخترشناسی و فیزیک زمینی را از بین می‌برد و مجموعۀ اصول واحدی را پیش‌فرض قرار می‌دهد که رفتار هر دو را توضیح می‌دهد. آن‌قدر عادت کرده‌ایم که فیزیک را با این جهان‌شمولیت در نظر بگیریم که درک اهمیت حیاتی این دگرگونی مستلزم تلاش است. یکی از نقاط اوج در «ساختار استدلالی اصولی» زمانی است که محاسبات نیوتن نشان می‌دهد نیرویی که ماه را در مدارش به‌دور زمین نگه می‌دارد دقیقاً مشابه نیرویی است که موجب سقوط یک سیب از درخت می‌شود. نیوتن اشتراک در ساختار فیزیکی را پیش‌فرض قرار می‌دهد، درحالی‌که فیزیکدان‌های ماقبل او ساختارهای فیزیکی را از اساس گوناگون پنداشته بودند.

مهم‌تر آن‌که، نیوتن، برخلاف ارسطو، هیچ حرکت طبیعی خاصی به اجسام نسبت نمی‌دهد. در عوض، قانون لختی حاکی از گرایش ذاتی هر جسم به باقی‌ماندن در حالت حرکتش -هر حالتی که باشد- است. برخلاف توصیف ارسطو، که مثلاً یک سنگ به‌سمت مرکز جهان هدایت می‌شود، [از نظر نیوتن] در جهان هیچ مکانی وجود ندارد که هر جسمی به‌طور ذاتی به آن سو جهت یابد. نظریۀ نیوتن مستلزم آن نیست که فضا نقطه مرکزی خاصی داشته باشد.

عرصۀ حرکت برای نیوتن موجودی است که او آن را فضای مطلق می‌نامد. به عقیدۀ نیوتن، حرکت تغییر جا در این فضاست. نقش فضای مطلق در نظریۀ نیوتن بسیار عمیق و فراگیر است، به‌طوری که سر درآوردن از هرچه او می‌نویسد بدون پذیرفتن وجود فضای مطلق غیرممکن به‌نظر می‌رسد.

 

زمان مطلق و پایندگی فضای مطلق

نیوتن بر این باور بود که نوعی عرصۀ فضایی با ساختار هندسی وجود دارد. او معتقد بود که این فضای سه‌بعدی نامحدود در هر لحظه از زمان وجود دارد. او به چیزی مبهم‌تر و جنجالی‌تر نیز اعتقاد داشت و آن این که نقاط فضا با گذر زمان عیناً بر جای می‌مانند.

قانون اول نیوتن بیان می‌کند که اگر هیچ نیرویی به یک جسم وارد نشود، آن جسم اگر ساکن باشد، ساکن می‌ماند و اگر در حال حرکت باشد، به حرکت یکنواختش در یک خط راست ادامه می‌دهد. اگر نقاط منفرد فضا با گذر زمان بر جای می‌مانند پس حالت سکون را می‌توان به‌دقت توصیف کرد: وقتی جسمی در یک دورۀ زمانی نقاط همانندی از فضای مطلق را اشغال می‌کند، در حال سکون مطلق است. هم‌چنین اگر نقاط فضای مطلق با گذر زمان بر جای بمانند، پس هر جسم متحرک در فضای مطلق یک مسیر خواهد داشت؛ یعنی: مجموعۀ نقاطی در فضای مطلق که در یک دورۀ زمانی مفروض اشغال می‌کند. بنابراین برای پی‌بردن به «حرکت مستقیم در خط راست»، نقاط فضا نه‌تنها باید در گذر زمان برجای بمانند، بلکه باید ساختار مستوی نیز داشته باشند؛ بدین معنا که بتوان مسیر فضایی را به‌شکل خط راست یا منحنی تشخیص داد.

نیوتن ویژگی دیگری به زمان مطلق نسبت می‌دهد. این که زمان، برخلاف فضا، جهت دارد. نیوتن دربارۀ جهت‌دار بودن زمان هیچ اظهارنظر روشنی نمی‌کند، و جهت‌دار بودن زمان مستقیماً به فهم قوانین او دربارۀ حرکت مربوط نمی‌شود. لیکن کاملاً طبیعی است که بگوییم زمان از گذشته به آینده می‌رود؛ و ارزش آن را دارد که در این‌جا به آن اشاره شود، زیرا بعداً به پرسش‌هایی در مورد جهت زمان باز خواهیم گشت.

نیوتن نیک آگاه است که این بخش‌های پایندۀ فضای مطلق را نمی‌توان به‌وسیلۀ حواس مشاهده کرد. هیچ مشاهده‌ای نمی‌تواند معلوم کند که آیا جسم در همان ناحیه از فضای مطلق توقف می‌کند یا مدام از ناحیه‌ای به ناحیۀ دیگر حرکت می‌کند. پس به‌نظر می‌رسد که حتی اگر قانون اول نیوتن صادق باشد و حتی اگر معلوم شود که هیچ نیرویی به جسم وارد نمی‌شود، هیچ مشاهده‌ای نمی‌تواند قانون اول نیوتن را تصدیق کند. و مهم‌تر آن‌که اگر نتوانیم فضای مطلق را مشاهده کنیم و به‌طریق اولی نتوانیم حرکت مطلق را درک کنیم، معلوم نیست نظریه‌ای که دربارۀ چنین حرکت مطلقی است اصلاً چگونه می‌تواند دربارۀ واقعیت مشاهده‌پذیر پیش‌بینی‌ای کند.

نیوتن مفاهیم «مطلق، حقیقی و ریاضی» فضا، زمان، مکان و حرکت را از مفاهیم «نسبی، ظاهری و معمولی» فضا، زمان، مکان و حرکت متمایز می‌کند. گرهِ مسئله آن است که وقتی قوانین حرکت نیوتن برحسب مفاهیم مطلق بیان شوند، مستقیماً مشاهده نمی‌شوند. وقتی سعی می‌کنیم حرکت شیئی را مشاهده کنیم، فقط می‌توانیم حرکت نسبی آن را مستقیماً بینیم، یعنی تغییر موقعیتش نسبت به دیگر اشیاء مشاهده‌پذیر، با آهنگ تغییری که به‌وسیلۀ حرکت مشاهده‌پذیر ساعت‌ها یا دیگر ابزارهای گویای زمان اندازه‌گیری می‌شود. اما اگر حرکت مطلق شیء به این دلیل غیرقابل درک باشد که فضا و زمان مطلق غیرقابل درک‌اند، مسلم انگاشتنِ موجودیت‌هایی از این دست چه ارتباطی با علم طبیعی می‌تواند داشته باشد؟ نیوتن بخشی از حاشیه‌نوشت پرینکیپیا را به پاسخ این پرسش اختصاص می‌دهد:

‌‌  ‌

اما قبل از پرداختن به قانون دوم باید درنگ کنیم و ببینیم که اگرچه فضا و زمان مطلق مستقیماً مشاهده نمی‌شوند، روایت نیوتن از فضا و زمان مطلق تا چه اندازه از لحاظ شهودی عمیق است. چنان‌که گویی نیوتن برخی موجودیت‌های عجیب، خیالی و ناآشنا را مسلم فرض می‌کند، اما اغلب مردم دنیای فیزیکی را برحسب فضا و زمان مطلق درک می‌کنند. مثلاً، صنعتگران و دانشمندان پیوسته می‌کوشند طراحی ساعت‌های مچی یا دیواری را بهبود بخشند تا ساعت‌هایی تولید کنند که هرچه بیشتر درست و دقیق باشند. اما چه چیزی باعث می شود یک ساعت دقیق باشد؟ برای این کار باید تیک‌های متوالی ساعت در بازه‌های زمانی یکسان ایجاد شود، یا عقربۀ ثانیه‌شمارِ ساعت دایره‌اش را با آهنگی ثابت طی کند. اما «یکسان» یا «ثابت»، با توجه به چه چیزی؟ با توجه به گذر خود زمان، یعنی، زمان مطلق. ما به‌طور طبیعی و شهودی مشاهده می‌کنیم که مقدار معینی از زمان مطلق بین دو تیک متوالی یک ساعت طی می‌شود و ساعت دقیق‌تر و بهتر ساعتی است که این بازه‌هایش شباهت بیشتری با یکدیگر داشته باشند. ساعت‌سازان سوئدی و طراحان ساعت‌های اتمی سعی می‌کنند ابزارشان را وادارند که چیزی را به‌دقت اندازه‌گیری کند که نوعی زمان مشاهده‌پذیر نسبی نیست. در فیزیک، هر حرکت فیزیکی مشاهده‌پذیر را (چرخش زمین، حرکت زمین به‌دور خورشید و الی آخر) در معرض اختلال تلقی می‌کنند و بنابراین خودبه‌خود یکنواخت نیست. اما غیریکنواختی را با نظر به حرکات مشاهده‌پذیر تعریف نمی‌کنند. این الزام در طراحی ساعت دیده می‌شود، زیرا عوامل اغتشاش حذف یا تصحیح می‌شوند. حذف عوامل اغتشاش تلویحاً نوعی اندازه‌گیری خود زمان را فرض می‌گیرد که معیار یکنواختی را به‌دست می‌دهد.

به‌طور مشابه، درک هرروزۀ ما از دنیا با معیار فضای مطلق است. هیچکس مثلاً از شنیدن این مسئله متحیر نمی‌شود که مدار زمین بیضی‌ای است که خورشید در یکی از کانون‌هایش قرار دارد. در کتابی علمی هر تصویری از منظومۀ شمسی مدارهای سیارات را نشان می‌دهد. اما این مدار دقیقاً بناست تصویر چه چیزی باشد؟ در هر لحظۀ مفروض، زمین در یک جاست. «مدار» به نحوی مجموعه‌ای از همۀ مکان‌هایی است که زمین در مدت یک سال اشغال می‌کند. لیکن این امر حاکی از آن است که مکان‌هایی که زمین در مواقع مختلف اشغال می‌کند، همه بخش‌هایی از یک فضای سه‌بعدی متداول یعنی فضای مطلق هستند. می‌توانیم با تلاش و تأمل دقیق دریابیم دنیا چگونه می‌توانست بدون هر نوع فضای مطلق یا حرکت مطلق وجود داشته باشد. اما با این کار نه‌تنها نظریۀ نیوتن، بلکه عقل سلیم را نیز انکار می‌کنیم.

نیوتن برای تصدیق عقایدش دربارۀ فضا و زمان مطلق به عقل سلیم متوسل نشد، او به آزمایش متوسل شد. نیوتن به‌جای تجزیه و تحلیل مفهومی، سعی کرد وجود حرکت مطلق را در آزمایشگاه اثبات کند. این موضوع، عنوان مبحث بعدی ماست…

قانون دوم نیوتن و آزمایش سطل آب

قانون اول نیوتن، برای اجسامی است که تحت تاثیر هیچ نیروی بیرونی‌ای واقع نشده باشند. اغوا می‌شویم که بگوییم نیوتن فرض می‌کند که این اجسام «در همان حالت حرکت باقی می‌مانند» اما این فرمول‌بندی جنبۀ اساسی و انقلابی این قانون را نادیده می‌گیرد: قانون اول دقیقا مشخص می‌کند چه چیزی «همان حالت اول حرکت» محسوب می‌شود.

جالب است بدانید قبل از نیوتن، گالیله نیز به دنبال مشخص کردن حرکت لختی اجسام زمینی بود، یعنی حرکت اجسام وقتی تحت تاثیر هیچ نیرویی نیستند و نتیجه گرفت که حرکت لختی، حرکت یکنواخت دایره‌ای است. او با آزمایش‌هایی که با سطح شیبدار انجام داد به این نتیجه رسید. گالیله متوجه شد که اگر توپی از یک سطح شیبدار پایین بیاید و بعد از یک سطح شیبدار دیگر بالا برود، تقریبا تا همان ارتفاع اولیه بالا می‌رود. مطابق شکل، هرچه زاویه کوچک و کوچک‌تر شود، توپ مجبور می‌شود روی سطح شیبدار دوم مسافت بیشتری را طی کند تا به ارتفاع اولیه برسد. بنابراین در زاویۀ صفر که توپ هیچ وقت به ارتفاع اولیه نمی‌رسد (در غیاب اصطکاک) تا ابد با سرعتی ثابت به حرکتش ادامه خواهد داد.

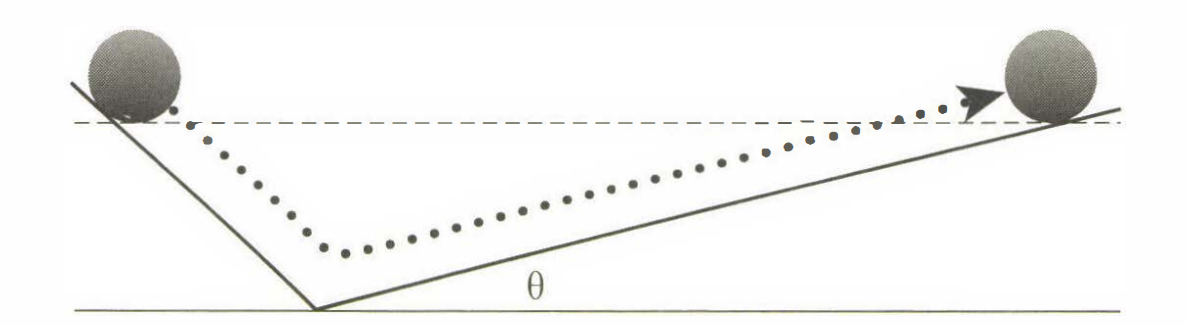
حرکت با سرعت ثابت که ارتفاع آن هرگز کم یا زیاد نشود، نوعی حرکت دایره‌ای یکنواخت است حول مرکز زمین. به یقین توپ تا ابد به حرکت روی یک خط راست ادامه نخواهد داد؛ خط راست مماس بر سطح زمین از زمین خارج می‌شود و سربالا می‌رود. پس توپ سعی می‌کوشد با دنبال کردن یک مسیر مستقیم سرعت خود را کم کند، سپس متوقف می‌شود و تا نقطۀ شروعش پایین می‌آید.

نوآوری نیوتن صرفا این فرض مسلم نیست که در غیاب نیروی بیرونی جسم گرایش به حفظ حرکت لختی‌اش دارد، بلکه، مدعی است که این حرکت، حرکت یکنواخت در خط راست است. اما این واضحا این قانون برای جهان پیرامون ما کافی نیست: ما هرگز اجسامی را که پیوسته در حال حرکت یکنواخت روی خط راست باشند، نمی‌بینیم. قانون دوم قانون اول را تکمیل می‌کند:

قانون دوم: تغییر در حرکت متناسب با نیروی محرک اعمال می‌شود و در راستای خط مستقیمی است که این نیرو بر آن اعمال می‌شود.

تغذیۀ قانون دوم از قانون اول مشخص است؛ بدون تعریف حالت حرکت در قانون اول، نمی‌توانستیم درکی از تغییر حرکت در قانون دوم داشته باشیم.

رابطۀ نیروها با تغییرات در حرکت مطلق نیوتن کلید فهم قوی‌ترین استدلال نیوتن به نفع حرکت‌های مطلق و، به طور عام‌تر، به نفع فضا و زمان مطلق را به دست می‌دهد. درست است که حرکت‌های مطلق اجسام مستقیما مشاهده نمی‌شود، اما گاهی اوقات نیروهای وارد بر اجسام قابل مشاهده هستند و جایی که نیروی خالص وجود داشته باشد، طبق قانون دوم، تغییری در حرکت مطلق به وجود می‌آید. برای روشن شدن ارتباط نیرو و تغییر در حرکت مطلق، نیوتن آزمایش بسیار ساده و متداولی پیشنهاد می‌کند که نیازی نیست عملا انجام داده شود. سطلی را پر از آب کنید، آن را با یک طناب از سقف آویزان کنید و طناب را به شدت بپیچانید. به محض رها کردن، طناب شروع به باز شدن می‌کند و آزمایش در چهار مرحله پیش می‌رود:

‌

این آزمایش تدارکات لازم را برای نیوتن فراهم آورد تا به روایت نسبی‌گرایانۀ حرکت، که دکارت و ارسطو از آن حمایت می‌کردند، حمله کند. یکی از مشکلات آشکار نظریۀ نسبی‌گرایانۀ حرکت آن است که هر جسم حرکت‌های نسبی متمایز زیادی دارد، زیرا می‌توان آن را با بسیاری از اجسام دیگر سنجید. اما فیزیک حرکت ایجاب می‌کند که برای یک جسم فقط یک حرکت خاص وجود داشته باشد، یعنی حرکتی که با قانون‌های فیزیک درک شود. ارسطو و دکارت حرکت فیزیکی جسم را به نسبت به چیزی که جسم را احاطه کرده بود ارجاع می‌دادند. اگر این را برای آزمایش سطل آب در نظر بگیریم، خواهیم دید که آب قبل از شروع آزمایش نسبت به سطل ساکن است و سطح آن تخت است، از طرفی در نهایت که آب و سطل با هم می‌چرخند، باز هم نسبت به هم ساکن اند ولی این بار سطح آب مقعر است؛ این تقعر نشان‎دهندۀ یک تفاوت فیزیکی است. حدس می‌زنیم که این تفاوت از آن ناشی می‌شود که آب در حالت اول نمی‌چرخد ولی در حالت بعدی می‌چرخد، اما حرکت آب، حرکت نسبت به سطل یا نسبت به جسمی که آن را احاطه کرده است نمی‌تواند باشد.

نسبی‌گرایان پاسخ می‌دهند که حرکت آب نسبت به سطل نیست، ولی به هر حال باز هم نسبی است؛ نسبت به اتاق، زمین یا ستارگان ثابت. اما نیوتن در انتهای حاشیۀ کتاب پرینکیپیا، ناب‌ترین مثال ممکن را برای آثار مشاهده‌پذیر حرکت مطلق در غیاب هر حرکت نسبی ارائه می‌دهد:

‌

کشش قابل مشاهده در ریسمان حتی وقتی که هیچ حرکت نسبی در کل عالم وجود ندارد، مبین دوران مطلق گوی‌هاست. آزمایش سطل آب نیوتن با همۀ سادگی‌اش یکی از قدرتمندترین و کوبنده‌ترین آزمایش‌ها در تاریخ فیزیک است. رفتار آب داخل سطل یا کشش ریسمانی که گوی‌ها را به هم وصل می‌کند، واقعیت مشاهده‌پذیری است که باید توجیه شود. توجیه معقولی به ذهن ما می‌رسد این است که چون دستگاه در حال چرخش است، آب به سمت لبه‌های سطل بالا می‌آید و ریسمان کشیده ‌می‌شود. اما چرخش نوعی حرکت است، پس باید بپرسیم نسبت به چه چیزی؟ نیوتن پس از استدلال خود مبنی بر این‌که این حرکت نسبت به محیط مجاور نیست، نتیجه می‌گیرد که حرکت باید نسبت به فضای مطلق باشد: اجسام در حال چرخش متوالیا جاهای مختلفی را در خود فضا اشغال می‌کنند. بدین ترتیب ارتباطی میان حرکت‌های مطلق و نیروها و در نتیجه آثار مشاهده‌پذیر وجود دارد.

 

حساب، هندسه و دستگاه‌های مختصات

در این کتاب قانون اول و دوم را بدون استفاده از حتی یک معادلۀ ریاضی (مثلا \(F=ma\)) ارائه دادم. این به این دلیل است که نیوتون نیز از معادله استفاده نکرد. او نظریه‌اش را به صورت هندسی ارائه داد و در پرینکیپیا قضیه‌ها را با تکنیک‌های هندسۀ اقلیدسی اثبات کرد. نیوتن فیزیکش را به صورت هندسی ارائه داد، زیرا موضوع خودش (یعنی حرکت در فضا) هندسی است.

مثلا گفتم که نیوتن ساختار هندسی فضای مطلق را \(E^3\) پیش‌فرض گرفت. اگر این فرض درست باشد، پس به کار بردن هندسۀ اقلیدسی روشی مستقیم برای استخراج واقعیت‌های مهم فیزیکی است. اما فیزیک مدرن هرگز در چارچوب هندسۀ اقلیدسی ارائه نشده است، بلکه به صورت جبری، بر حسب اعداد و معادله‌های عددی ارائه می‌شود. مثلا در یک کتاب فیزیک معمولی هیچگاه به فضای مطلق سه‌بعدی اقلیدسی \(E^3\) اشاره نمی‌شود، در عوض به \(R^3\) اشاره می‌شود و \(R^3\) معنی ریاضی خاصی دارد. \(R^3\) مجموعه‌ای از اعداد حقیقی سه‌تایی مرتب است. هر عضوی از \(R^3\) به شکل \((x,y,z)\) است که هر یک از متغیرها علامت اختصاری برای یک عدد حقیقی خاص است. به‌علاوه \(R^3\) تا حد زیادی ساختاری ریاضی دارد که هیچ شباهتی به \(E^3\) ندارد. مثلا، برای هر دو عضو مفروض \(R^3\) می‌توان پرسید عددهای اول و دوم یکسان هستند یا نه، هم‌چنین برای هر دو جفت عضور مفروض \(R^3\) می‌توان جمع آن‌ها  \((x_1+x_2,y_1+y_2,z_1+z_2)\) را به سادگی پیدا کرد و می‌توان درک کرد که ضرب هر یک از آن‌ها در یک اسکالر چه معنایی دارد. اما هیچ یک از این عملیات‌ها نظیری برای نقطه‌های واقع در \(E^3\) ندارند. حال چطور می‌شود که این دو به راحتی با هم اشتباه می‌شوند؟

جواب در کاربرد دستگاه مختصات نهفته است. دستگاه مختصات \(E^3\) تناظری یک‌به‌یک بین اعضای \(E^3\) (نقاط هندسی) و نوعی ابژۀ عددی ایجاد می‌کند. به‌ طور معمول از اعضای \(R^3\) به عنوان مختصات \(E^3\) استفاده می‌کنیم. مزیت به کار بردن نمایش عددی برای اعیان هندسی آن است که به ما امکان می‌دهد روش‌های جبری را برای حل مسائل هندسی به کار بریم. با یک دستگاه مختصات می‌توان مسائل هندسی را به مسائل عددی تبدیل کرد و آن‌ها را با روش‌های عددی حل کرد. اما ممکن است در تمایز میان اشیاء هندسی و نمایش دوبارۀ آن اشیاء ابهام به وجود آید. این نگرانی بی‌مورد نیست. اینشتین نیز در یادداشت‌های مربوط به زمان طولانی‌ای که نظریۀ نسبیت را در سر می‌پروراند می‌گوید:

‌‌

حتی اینشتین هم روزگار سختی را گذراند تا ویژگی‌های مختصاتی را که مفهوم هندسی یا فیزیکی دارند را از آن‌هایی که ندارند، تمیز دهد.

وقتی که دستگاه مختصات برای فضا انتخاب شه، قوانین دینامیکی را می‌توان به شکل جبری نسبت به آن مختصات بیان کرد. این همان چیزی است که در کتاب‌های فیزیک معاصر برای ارائۀ مکانیک نیوتنی مرسوم است؛ برای مثال کتاب مکانیک کلاسیک گلدشتاین را در نظر بگیرید:

‌

به زعم گلدشتاین، قانون دوم حرکت نیوتن به نحو بسیار قابل توجهی چیزی دربارۀ «چارچوب‌های مرجع» می‌گوید. اما، همانطور که دیدیم، نیوتن قانون دوم را بدون هیچ اشاره‌ای به چارچوب مرجع بیان می‌کند. در واقع او هیچ ایده‌ای دربارۀ آنکه «چارچوب مرجع» چیست نداشته است. همچنین بسیار قابل توجه است که گلدشتاین به نحوی بدون اشاره به قانون اول به قانون دوم پرش می‌کند، اما همانطور که دیدیم قانون دوم نیوتن برای آنکه محتوا داشته باشد باید قانون اول را پیش‌فرض بگیرد.

 

تقارن‌های فضا و مباحثات لایب‌نیتس و کلارک

اگرچه نیوتن ساختار فضا را \(E^3\) فرض می‌کند، در دینامیک نیوتن هیچ‌چیز مستلزم این فضا نیست و انتخاب خاص فضای \(E^3\) موجب اعتراضاتی به نظریۀ نیوتن شده است.
فضای سه‌بعدی اقلیدسی، نشان‌دهندۀ میزان بالای تقارن است. فضایی که تقارن انتقالی دارد، همگن و فضایی که حول یک نقطه تقاران دورانی دارد، همسانگرد نامیده می‌شود. در یک فضای همگن همه‌جا «یکسان به نظر می‌رسد». شما می‌توانید هرچیزی را در فضا جابه‌جا کنید و نسبت‌های هندسی یکسان بین آن‌ها را حفظ کنید. اگر فضایی در یک نقطه همسانگرد باشد، در آن نقطه تمام جهت‌ها «یکسان به نظر می‌رسد». هر چیزی را می‌توان با دوران حول آن نقطه دوباره جهت داد و همچنان تمام نسبت‌های هندسی را حفظ کرد. این تقارن‌ها به نحو ضمنی در هندسۀ اقلیدسی مسلم گرفته شده‌اند: باید بتوانیم هر نمودار اقلیدسی را ترسیم کنیم و نتایج یکسان به دست آوریم، بی‌آن‌که اهمیت داشته باشد که کاغذ کجای دنیا باشد یا در چه جهتی باشد.

یکی از پیامدهای این تقارن \(E^3\) آن است که در \(E^3\) ماده می‌تواند به روش‌های مختلف توزیع یابد ولی همۀ موقعیت‌های نسبی یکسان حفظ شود. هر توزیعی از ماده را که در نظر بگیرید و تمام آن را با فاصلۀ ثابتی انتقال دهید، یا به همان میزان حول یک محور دوران دهید، موقعیت‌های مکانی نسبی اشیاء تغییر نمی‌کند. اگر خود ماده توزیع متقارن یکسان نداشته باشد، توزیع جدید آن با قبلی متفاوت است، اما همۀ موقعیت‌های مکانی نسبی ثابت باقی می‌مانند.

گوتفید لایب‌نیتس و ساموئل کلارک در نامه‌نگاری‌های غیرمستقیم و معروفشان، دربارۀ قابل قبول بودن فیزیک نیوتن بحث و گفتگو کردند. در ابتدا، موضوع بحث آن بود که آیا فیزیک نیوتن باورهای مذهبی را تضعیف می‌کند؟ در این مباحثات لایب‌نیتس فلسفۀ خودش را تبلیغ و ادعا می‌کند که فقط با یک اصل واحد، یعنی اصل جهت کافی (PSR: Principle of Sufficient Reason) متافیزیک را تا حد یک علم روشنگر مطرح کرده است:

‌

به نظر می‌رسد کلارک با لایب‌نیتس موافق است اما سخت در فکر است که شرح دهد چگونه ارادۀ خداوند باید علت غایی امور باشد که ناگهان با مثالی سرنوشت‌ساز روبه‌رو می‌شود:

‌‌

کلارک می‌گوید وقتی خدا ماده را می‌آفرید اصلا می‌توانست کل نظام مادی را در هر مکان دیگری در فضای مطلق قرار دهد، «تمام مکان‌ها مطلقا برای ماده تفاوتی نداشت». تقارن فضای اقلیدسی این اطمینان را می‌دهد که این نظام مادی را بتوان در هر مکانی و با هر جهتی قرار داد. پس طبق نظر کلارک، خداوند باید از میان انواع راه‌های ممکن برای پر کردن فضای مطلق با ماده دست به انتخاب بزند. کلارک اصرار دارد که «ارادۀ محض خداوند» باید عامل تعیین‌کننده باشد، زیرا هیچ‌یک از این موارد ممکن توزیع ماده بر دیگری رجحان ندارد.
لایب‌نیتس بی‌درنگ این مکاتبه را از سر می‌گیرد:

‌‌

در این برهان علاوه بر PSR، از مفروضات دیگری نیز استفاده شده است. فرضی که بیش از همه قابل توجه است آن است که وجود و ساختار هندسی فضای مطلق مستقل از هر ماده‌ای است. پس امکان دارد که فضا کاملا تهی از اشیای مادی، یعنی به شکل یک خلأ کامل، وجود داشته باشد. خلأ عدم ممکن نیست بلکه فضای خالی است و بنا بر نظر نیوتن در واقع، چنین فضای خالی‌ای به مدت نامحدود، قبل از آنکه خداوند هیچ ماده‌ای در آن خلق کند، وجود داشته است.

فرض دیگر برهان فوق، تقارن فضای مطلق است. در فضای کروی ارسطو، این تقارن (همگنی و همسانگردی در تمام نقاط) وجود ندارد، پس در این فضا جهتی (علتی) برای قرار دادن اشیا در مرکز فضا وجود دارد و نه لبۀ آن. در برهان لایب‌نیتس، توسل به تقارن‌ها هرگز به چالش کشیده نمی‌شود چون لایب‌نیتس و کلارک هر دو فرض کرده اند که فضا \(E^3\) باشد. اما اگر این فرض کنار گذاشته شود و فضایی در نظر گرفته شود که فاقد این تقارن‌ها باشد، برهان PSR دیگر نمی‌تواند از ارائۀ دلیل شانه خالی کند. وقتی به بحث نسبیت عام برسیم، خواهیم دید که این برهان نظرورزی بی‌پایانی نیست.

لایب‌نیتس در حمله به نیوتن استدلال دیگری به کار می‌گیرد که از مقدماتی کاملا متفاوت ساخته شده است. جدا کردن این دو برهان از هم مستلزم توجه منظم است.

ادامۀ نقل قول:

‌ ‌

جملۀ آخر مسئلۀ جدیدی را مطرح می‌کند که نه بر اساس PSR بلکه بر اساس اصل این‌همانی تمایزناپذیرهای لایب‌نیتس (PII: Principle of Identitiy of Indiscernibles) است. بر اساس گفتۀ لایب‌نیتس می‌توان تصور کرد که همۀ ماده از جایی برداشته شود و در جای دیگری در فضا قرار داده می‌شود. اما این دو هیئت متفاوت ماده در فضای مطلق به معنایی بدیهی «کاملا یکسان به نظر می‌رسند»و هیچ توصیف کیفی‌ای نمی‌تواند آن‌ها را از هم متمایز کند. اما بر اساس اصل PII، دو شیء متمایز که از یکدیگر قابل تشخیص نباشند، نمی‌توانند وجود داشته باشند.

اگر اصل PII را بپذیریم، اغلب روایت در باب ماده، مستقل از ملاحظات فضایی منتفی می‌شوند. لایب‌نیتس خودش تصور می‌کند که PII با نظریۀ اتمی ماده مغایرت دارد، زیرا فرض می‌شود اتم‌های منفرد باید از نظر کیفی یکسان باشند. البته در فیزیک مدرن این اصل الزامی ندارد، زیرا دو اتم هیدروژن در حالت پایه از نظر کیفی کاملا یکسان هستند. بنابراین مهم‌ترین سوال دربارۀ برهان PII این است که اصلا چرا باید آن را بپذیریم؟ مخالفت با این اصل بیشتر از جنبۀ معرفت‌شناختی است تا متافیزیکی یا معناشناسی. اگر دوشیء تمایزناپذیر وجود داشته باشد، پس نمی‌توانیم بگوییم که کدام‌یک، کدام بود. در این صورت سوال‌های مشخصی وجود خواهند داشت که با هیچ مشاهده‌ای نمی‌توان به آن‌ها پاسخ داد.

نیوتن واقعیت‌های مشاهده‌پذیر را با واقعیت‌های نسبی و محسوس، مانند موقعیت مکانی و سرعت یک ذرۀ مادی مشاهده‌پذیر نسبت به دیگری یکسان در نظر می‌گیرد. اما نوع مطلق آن‌ها به همان روش مشاهده‌پذیر نیستند و رابطۀ بین واقعیت‌های مشاهده‌پذیر و مشاهده‌ناپذیر کاملا واضح است. لایب‌نیتس در عوض معتقد است که فیزیک مستقیما بر حسب کمیت‌های نسبی نیوتن، یعنی موقعیت‌های مکانی و سرعت‌های نسبی اشیاء تدوین شود. لایب‌نیتس می‌خواهد بخش‌های مشاهده‌پذیر وجودشناسی نیوتن را بردارد و مابقی را کنار بگذارد.

اما در فیزیک آشکارا وجودهای مشاهده‌ناپذیر همچون اصل موضوع پذیرفته می‌شوند تا رفتارهای مشاهده‌پذیر تبیین شوند. با این همه، حرکت مطلق نیوتنی که مشاهده نمی‌شود، به شکل خاصی آزاردهنده است. درک این فرض، که مکان در فضای مطلق مشاهده‌پذیر نباشد، دشوار است زیرا معلوم نیست که مشاهده ممکن است چه نوع اطلاعاتی را بیان کند. در ادامه با بررسی این‌که چگونه می‌توان واقعیت‌های مشاهده‌ناپذیر نیوتن را با تغییر وجودشناسی فضا و زمان حذف کرد، مطالب بسیاری خواهیم آموخت…

سرعت مطلق و نسبیت گالیله‌ای

در فصل قبل روی مباحثۀ اول کلارک و استفادۀ لایب‌نیتس از آن علیه خود کلارک تمرکز کردیم. کلارک معتقد است که امور واقع در فضا باید فراتر از صرف روابط فضایی میان اجسام باشد، زیرا اجسامی که روابط فضایی یکسان دارند ممکن است به نحوی متفاوت در فضای مطلق قرار داده شوند؛ لایب‌نیتس نیز پاسخ می‌دهد که فضای مطلق نمی‌تواند وجود داشته باشد زیرا (1) خداوند نمی‌تواند از میان امکان‌های متفاوتی که کلارک ذکر کرده است، اگر وجود داشته باشند، دست به انتخاب بزند (PSR) و (2) نمی‌توان امکان‌هایی مختلف را که از نظر کیفی کاملا یکسان باشند از هم تمیز داد (PII). وقتی لایب‌نیتس هر نوع تفاوت فیزیکی واقعی بین دو موقعیت را انکار کرد، کلارک قانع نشد و مثال دیگری آورد که در آن دو موقعیت فیزیکی متفاوت موقعیت‌های نسبی یکسانی را برای اجسام مادی به وجود می‌آورند:

‌

این مثال کلارک مربوط به سرعت مطلق ماده در فضاست. لایب‌نیتس به این استدلال، مشابه همان روش قبلی پاسخ می‌دهد، یعنی با کاربرد همزمان برهان‌های PSR و PII:

‌

دو استدلال لایب‌نیتس این‌گونه است: (1) در واقع در اینجا دو امکان متفاوت وجود ندارد، یکی جهان مادی ساکن و دیگری جهانی که در یک خط راست در حال حرکت یکنواخت است (PII) و (2) با وجود غیرممکن بود، اگر دو امکان متفاوت وجود می‌داشت، خداوند هیچ دلیلی برای انتخاب یکی از آن‌ها نداشت (PSR). اما پس از تامل خواهیم دید که به همین سادگی هم نمی‌توان از PSR علیه کلارک استفاده کرد. فرض کنید خدا در هنگام آفرینش جهان مادی در یک فضای خالی، قصد داشت به کل جهان سرعتی مشخص در یک جهت دهد. برای این امر وی باید یک جهت را انتخاب می‌کرد، اما تقارن E3 ایجاب می‌کرد که همۀ جهت‌ها از نظر کیفی یکسان باشند. تنها سرعت مطلقی که لازم نیست یک جهت از میان جهت‌ها برای آن انتخاب شود، سرعت صفر یعنی سکون مطلق است. پس PSR نه‌تنها مانع از هرگونه انتخاب سرعت مطلق برای جهان می‌شود بلکه مسلزم دقیقا یک انتخاب است.

از طرف دیگر برهان PII منجر به نتایج جالبی می‌شود. اول از همه لایب‌نیتس و کلارک هردو موافق‌اند که حرکت مستقیم‌الخط یکنواخت یک سیستم مادی در فضای مطلق به مشاهده درنمی‌آید. چنین سیستمی حرکت‌های نسبی یکسان اجزایش را، و از همین رو رفتار قابل مشاهدۀ یکسانی را نشان خواهد داد، چنان‌که گویی در سکون مطلق به سر می‌برد. گالیله از این ادعا که به صورت شهودی آشکار نیست، دفاع کرده است.

هنگام بحث دربارۀ نظام کوپرنیکی، گالیله باید توضیح می‌داد که چرا حرکت بسیار سریع سطح زمین هنگام چرخش حول محورش، و حتی حرکت سریع‌تر زمین در مدارش به دور خورشید، با مشاهدۀ عادی آشکار نمی‌شوند. گالیله خاطرنشان کرد که، در شرایط خاص، حرکت مطلق یک نظام روی رفتار مشاهده‌پذیر درون نظام تفاوتی به وجود نمی‌آورد. او مثال می‌آورد که اگر شما و دوستانتان به همراه چند پرنده، چند ماهی درون تنگ آب، درون کابین کشتی باشید، رفتار هیچ‌یک از این سیستم‌ها هنگام سکون و حرکت کشتی تفاوتی نخواهد داشت. برای مثال ماهی‌ها درون تنگ‌شان در هر جهتی به صورت دلخواه حرکت می‌کنند و هرگز اینطور نیست که در هنگام حرکت کشتی، تغییری در جهت حرکت ماهی‌ها پدید آید (حرکت پرنده‌ها نیز به همین نحو خواهد بود). حتی شما می‌توانید در هنگام سکون به هر جهت که می‌خواهید بپرید و در هنگام حرکت کشتی نیز با همان نیروی قبلی می‌توانید در هر جهت دلخواه جهش داشته باشید، علی‌رغم اینکه اگر در هنگام حرکت بپرید، سطح زیر پای شما در جهت حرکت کشتی به جلو خواهد رفت. این ادعا که همۀ آزمایش‌های انجام شده در دو حالت کشتی پیامد مشاهده‌پذیر یکسانی دارند، نسبیت گالیله‌ای نامیده می‌شود.

گالیله مانند نیوتن و کلارک بدیهی می‌گیرد که در هربار آزمایش حالت حرکت کشتی متفاوت است، اما نتایج آزمایش‌ها تمیزپذیر نیستند، زیرا موقعیت‌های مکانی نسبی و حرکت‌های نسبی همۀ اجسام در هر دو حالت یکسان است. به طور قطع، لایب‌نیتس بر اساس PII استدلال می‌کند که دو موقعیت واقعا متفاوت اصلا وجود ندارد. یا ترجیحا، لایب‌نیتس قبول می‌کند که در مثال گالیله کشتی نسبت به ساحل حالت‌های حرکت متفاوتی دارد، اما کلارک کلا به دنبال چیز دیگری است: اگر همۀ ماده در عالم در حرکت یکنواخت باشد، پس اصلا هیچ تفاوتی در حرکت نسبی وجود ندارد. لایب‌نیتس مدعی است که این امر مهمل است.

ایرادهای PII را همچون اصل بنیادین هستی‌شناسی یا متافیزیک قبلا مطرح کردیم اما پذیرفتیم که اصل موضوع قرار دادن واقعیت‌های فیزیکی مشاهده‌ناپذیر ما را دچار تردید می‌کند. تفاوت مباحثۀ اول کلارک با مباحثۀ دوم آن، یعنی تفاوت موقیت مکانی در فضای مطلق و حرکت مطلق در این است که اینک می‌توانیم پرسش‌های فیزیکی دربارۀ عالم مادی را فرموله کنیم، پرسش‌هایی که به عقیدۀ نیوتن جواب‌هایی معین دارند که به روش تجربی نمی‌توانیم آن‌ها را پیدا کنیم. این امر ما را دچار تردید خواهد کرد. آیا هیچ راهی وجود ندارد که به طریقی این سرعت‌های مطلق مشاهده‌ناپذیر را از نظریۀ نیوتن کنار گذاشت و درعین حال تمام قدرت تبیینی آن را حفظ کرد؟

برای هر دانشجوی فیزیک عبارت «چارچوب مرجع لخت» آشناست. اما معنی این عبارت دقیقا چیست؟ نیوتن چارچوب مرجع لخت را چنین توصیف می‌کند: یک جسم مشهود که در حالت سکون مطلق است یا بدون دوران، در یک مسیر مستقیم در فضای مطلق در حال حرکت یکنواخت است و موقعیت‌های مکانی و حرکت اجسام دیگر نسبت به آن سنجیده می‌شود. واضح است که این توصیف فضای مطلق را از فیزیک حذف نمی‌کند. بنابراین اگر بگوییم نسبیت گالیله‌ای ادعا می‌کند که «همۀ چارچوب‌های لخت یکسان‌اند» و سپس چارچوب لخت را به این روش تعریف کنیم، دقیقا دربارۀ فضای مطلق و حرکت مطلق با نیوتن هم‌عقیده‌ایم.

 

فضا-زمان گالیله‌ای

نیوتن فرض کرد که فضا ساختار E3 و زمان ساختار متریکی یک‌بعدی دارد و از همه مهم‌تر، فرض می‌کند که نواحی منفرد فضای مطلق در گذر زمان بر جای می‌مانند که این معیاری برای تشخیص سکون مطلق به ما می‌دهد. هر جسم در فضای مطلق مسیری دارد، که این مسیر ممکن است شکل‌های گوناگون مانند خط راست و یا بیضی داشته باشند. نیوتن با این هستی‌شناسی می‌تواند سکون مطلق و حرکت مطلق یکنواخت در یک خط راست را تعریف کند و بنابراین قانون اولش دربارۀ حرکت را بنویسد. اگر بخواهیم به طریقی دینامیکی نیوتن را حفظ اما توصیف وی از فضا و زمان را رد کنیم، به ساختارهای دیگری نیاز داریم که بتوان قانون اول نیوتن را برحسب آن تدوین کرد.

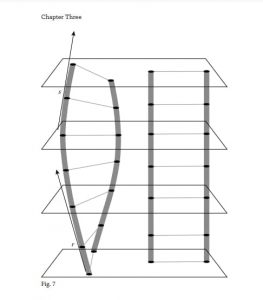
با بازنمایی هستی‌شناسی نیوتن شروع می‌کنیم. برای راحتی، به‌جای فضای سه‌بعدی فضای مطلق نیوتنی دوبعدی را ترسیم می‌کنیم. فرض کنید فقط دو جسم A و B در این فضا وجود دارند. در هرلحظۀ زمانی مفروض، اجسام در نقاط خاصی در فضای مطلق قرار گرفته‌اند. با گذر زمان، اجسام می‌توانند جایشان را در فضای مطلق تغییر دهند. شکل زیر اجسام را در چهار لحظۀ زمانی مختلف نمایش می‌دهد. به‌علاوه دو نقطه از فضای مطلق به نام p و q در هر چهار لحظه نشان داده شده‌اند.

اولین کاری که باید انجام دهیم، روی هم چیدن نمایش‌های فضای دوبعدی‌مان است. در این فرآیند دو قرارداد آشکار اما اساسی را به کار می‌بریم. اول آن‌که آن‌ها را طوری روی هم می‌چینیم که هر نقطه با گذر زمان در فضای مطلق خطی عمودی تشکیل دهد. دوم این‌که آن‌ها را طوری روی هم می‌چینیم که مسافت عمودی بین هر جفت رد متناسب با زمان مطلق سپری‌شده باشد. بنابراین اگر زمان سپری‌شده بین t=3، t=2، t=1، t=0 همه یکسان باشد، باید چهار رد با بازه‌های مساوی در فضا قرار داده شود. در نتیجه نمایش فضایی دوبعدی‌مان فضایی سه‌بعدی است که با گذر زمان ادامه می‌یابد. اکنون می‌توانیم موقعیت‌های مکانی هر جسم را با تشکیل جهان‌خط‌هایشان نشان دهیم. (مطابق شکل زیر)

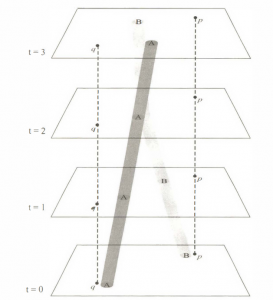
تاکنون اصلا روایت نیوتن دربارۀ فضا و زمان را تغییر نداده‌ایم؛ صرفا یک نمایش فضایی به دست داده‌ایم از ساختار فضایی و زمانی که نیوتن مفروض می‌گیرد. این نوع نمایش که در آن فضا و زمان هر دو با هم در یک نمودار نشان داده می‌شوند، نمودار فضا-زمان نامیده می‌شود. چون نقاط فضای مطلق در گذر زمان بر جای می‌مانند، می‌توانیم تعیین کنیم که چگونه برش‌های زمان را روی هم بچینیم و چون زمان مطلق ساختار متریکی دارد، می‌توانیم فاصلۀ بین برش‌های مختلف در فضا را تعیین کنیم. در نمودار فضا-زمان اجسامی که در حالت سکون مطلق به سر می‌برند، با خطوط عمودی نمایش داده می‌شوند زیرا آن‌ها در همان نقطۀ فضای مطلق باقی می‌مانند. اما مهم‌تر آن‌که، مسیرهای اجسامی که در فضای مطلق حرکت یکنواخت در یک خط مطلق دارند، با خطوط راست در نمودار فضا-زمان نمایش داده می‌شوند.

حال فرض کنید در یک فضای کاملا خالی دیگر دو جفت گوی که با ریسمان بسته شده‌اند، وجود دارد. یک جفت گوی در حالت سکون مطلق است و ریسمان هیچ کششی ندارد. جفت دیگر در حالت دوران مطلق حول مرکز جرمشان هستند و ریسمان دارای کشش است. شکل زیر نمودار فضا-زمان این دو جفت گوی را نمایش می‌دهد.

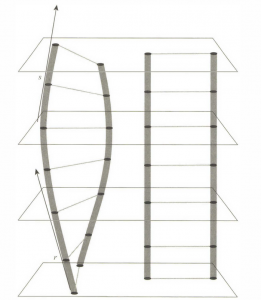
‌گوی‌های سمت راست در حالت سکون مطلق هستند و مسیرشان در نمودار با خطوط راست نمایش داده شده است. گوی‌های چرخان درست برعکس، پیوسته حالت حرکت مطلقشان را تغییر می‌دهند. روی نمودار این حرکت با انحنای جهان‌خط‌هایشان نشان داده شده است. سرعت مطلق یک گوی در هر لحظه متناسب با خط مماس به مسیر در آن نقطه است. سرعت مطلق یکی از گوی‌ها در نقاط r و s در نمودار بالا با دو خط مماس نمایش داده شده است. مقدار سرعت مطلق یک شیء با زاویۀ این خط مماس نشان داده می‌شود. تغییر مداوم خط‌های مماس با گذر زمان بیانگر شتاب گوی‌های سمت چپ است.

بر اساس چنین نمودارهایی می‌توانیم قانون اول نیوتن را چنین بازنویسی کنیم:

قانون اول (به روایت نمودار فضا-زمان): در یک نمودار فضا-زمان مسیر یک جسم با یک خط راست نمایش داده می‌شود، مگر این‌که جسم بر اثر نیروهای واردشده مجبور به تغییر حالتش شود.

توجه کنید در روایت جدید ما، هیچ تمایزی میان اجسام در حال سکون مطلق و اجسامی که حرکت یکنواخت دارند، وجود ندارد. هر کدام از این‌ها یک حرکت لخت است، یعنی حرکت جسم وقتی تحت تاثیر هیچ نیروی خارجی نباشد.

در این روایت، قانون دوم نیوتن چنین بیان می‌شود که اثر نیروی واردشده با انحنا یا خمیدگی جهان‌خط در نمودار نمایش داده ‌می‌شود. جهان‌خط در جهت نیروی وارد شده خم می‌شود و مقدار انحنای آن متناسب با مقدار نیروی وارد شده و نیز جرم جسم است. در قانون اول به جرم جسم، به ویژه جرم لختی جسم، اشاره نشده است زیرا هیچ نقشی در رفتار جسم آزاد از نیرو ندارد. در اصل، جرم لختی جسم اندازه‌گیری مقاومت جهان‌خط آن در برابر خم شدن بر اثر نیرو است؛ به طوری که مسیر جرم بزگ‌تر خمیدگی کمتری خواهد داشت.

آنچه در فرمول‌بندی مجدد قوانین نیوتن حائز اهمیت است آن است که هیچ اشاره‌ای به سرعت مطلق هیچ جسمی نمی‌شود؛ فقط کافی است مسیرهای مستقیم و خمیده را فضا-زمان از هم تشخیص دهیم. مادامی که این دو را بتوانیم از هم تشخیص دهیم، می‌توانیم بگوییم در هر حالت مفروض قوانین نیوتن چه چیزی را پیش‌بینی می‌کند. دیگر لازم نیست که مسیر نقاط منفرد فضای مطلق را بدانیم.

به چیزی که لازم نیست بدانیم، نیازی نداریم. پس اگرچه نیوتن فرض می‌کند نقاط نفرد فضای مطلق در گذر زمان بر جای می‌مانند، ما توانستیم قوانین نیوتن را بدون اشاره به پایندگی نقاط یا سرعت مطلق هر چیزی دوباره فرمول‌بندی کنیم. مختاریم که روایت نیوتن از فضا و زمان را به نفع روایت جدید آن رد کنیم. البته نمی‌توانیم پایندگی نقاط فضا در طول زمان را رد کنیم بی آن‌که بهای آن را در جایی دیگر پرداخت کنیم. باید کاری بیش از صرف حذف جزئی از متافیزیک انجام دهیم و برای افزودن آنچه ساختار هندسی ما به آن نیازد دارد، باید کل روایتمان از هستی‌شناسی فضا و زمان را تغییر بدهیم.

در هستی‌شناسی جدیدمان، روایت فضا و زمان مطلق و جداگانۀ نیوتن را به نفع نقاط فضا-زمان یا رویدادها رد می‌کنیم. یک رویداد در اصل یک مکان-در-فضا-در-یک-زمان است. در حالت ایده‌آل هیچ گسترش فضایی ندارد و آنا اتفاق می‌افتد، مانند انفجار آنی یک ترقه. وقتی بپذیریم رویدادها عناصر اصلی هستی‌شناسی فضا-زمانی ما هستند، کار ما مشخص کردن ساختار فیزیکی این رویدادها یا به عبارتی هندسۀ فضا-زمان است. در فضا-زمان گالیله‌ای چند نوع ساختار مختلف اصل موضوع فرض می‌شود.

نخست، بین هر جفت رویداد یک بازۀ زمانی مطلق عینی وجود دارد. با این تعبیر، فضا-زمان گالیله‌ای، زمان مطلق نیوتنی را بدون هیچ تغییری می‌پذیرد. با این تعبیر می‌توان فضا-زمان گالیله‌ای را به مجموعه رویدادهایی تقسیم کرد که بازۀ زمانی بین آن‌ها صفر باشد؛ برش‌های همزمان در فضا-زمان. با در نظر گرفتن این برش‌ها، فضا-زمان‌مان ساختاری لایه‌لایه به خود خواهد گرفت. حال در هر کدام از این برش‌های همزمانی، هندسۀ فضایی خاصی فرض می‌شود؛ رویدادهای در هر برش ساختار فضایی E³ دارند. در اینجا هندسۀ هر برش باید مستقل از برش‌های دیگر تعیین شود زیرا نقاط فضا دیگر در گذر زمان بر جای نمی‌مانند.

در روایت خود نیوتن از فضا و زمان دیدیم که زاویۀ مسیر بر روی نمودار، مفهوم فیزیکی دارد و سرعت مطلق جسم را نشان می‌دهد و اشیایی که در سکون مطلق به سر می‌برند مسیرهای عمودی را اشغال می‌کنند. اما در فضا-زمان گالیله‌ای هیچی سرعت مطلقی وجود ندارد. در نمودار، مسیرهای مستقیم را می‌توان به دلخواه عمودی یا کج ترسیم کرد. بنابراین نموداری که در قبل در فضا-زمان نیوتنی ترسیم شده بود را در فضا-زمان گالیله‌ای می‌توان مطابق شکل زیر بازترسیم کرد.

‌ساختار فضا-زمان گالیله‌ای در همۀ روایت‌های استاندارد پیش‌فرض مکانیک نیوتنی است، هرچند این پیش‌فرض اغلب ضمنی است و به آن اشاره نمی‌شود. فضا-زمان گالیله‌ای عرصه‌ای آرمانی را برای مکانیک نیوتنی فراهم می‌کند. این ساختار فضا-زمان برای بیان قوانین حرکت نیوتن، تمایز نظام چرخان از غیرچرخان و بنابراین برای توضیح پدیده‌های آزمایش سطل و تعریف دستگاه‌های مختصات لخت و نالخت بسنده است. اما در حالت کلی برای تعریف سکون مطلق یا سرعت مطلق کافی نیست. اگر مکانیک نیوتنی برای تبیین همۀ پدیده‌های مشاهده‌پذیر کفایت می‌کرد، فیزیکدان‌ها تقریبا با اطمینان فضا-زمان گالیله‌ای را به عنوان روایت درست ساختار فضا-زمانی انتخاب می‌کردند.

ساختار فضا-زمان به طور مستقیم مشاهده‌پذیر نیست اما به هر حال در شکل‌گیری نظریۀ فیزیکی نقش اساسی بازی می‌کند. هیچ ضرورتی ندارد که سعی کنیم ساختار فضا-زمان را از فیزیک حذف کنیم، همان‌طور که اصل موضوع اتم‌ها را فقط به خاطر این‌که  اتم‌ها مستقیما دیده نمی‌شوند، حذف نمی‌کنیم.

اما بدیهی است که با نظریۀ نیوتن همه‌چیز روبه‌راه نیست. هرچه تلاش کنیم نمی‌توانیم برخی از پدیده‌ها را، به ویژه پدیده‌هایی که شامل نور و الکترومغناطیس هستند را با نظریۀ نیوتن تبیین کنیم. در نتیجه مکانیک نیوتنی و همراه آن فضا و زمان مطلق نیوتنی و فضا-زمان گالیله‌ای هر دو به نفع نظریۀ نسبیت خاص کنار گذاشته می‌شوند.

‌

نسبیت خاص و فضا-زمان مینکوفسکی

نسبیت خاص نظریه ای بسیار ساده است که معمولا به شکلی پیچیده و گیج کننده ارائه می شود. برخی از دلایل این امر تاریخی هستند. خود اینشتین این نظریه را به مثابه پیامد دو اصل بیان کرد: (۱) هم ارزی تمام چارچوب های لخت و (۲) ثابت بودن سرعت نور. به یک تعبیر، از روی این دو اصل می توانیم تبدیلات لورنتس را به دست آوریم. تبدیلات لورنتس مجموعه معادلاتی هستند که یک مجموعه مختصات را به مجموعه ای دیگر ربط می دهند. اما به زودی خواهیم دید که این روش جداً ما را از درک نظریه نسبیت دور می کند.

اول آن که، مفهوم یک دستگاه لخت یا یک مجموعه مختصات لخت، یا یک چارچوب مرجع لخت، بیشتر اقتباسی است تا اینکه یک مفهوم اساسی باشد. برای آن که بفهمیم منظور از وابسته «لخت» چیست، هر یک از این مفاهیم را می توان تنها با ارجاع به نوعی ساختار هندسی عینی از خود فضا-زمان تعریف کرد. بنابراین باید با هندسه ذاتی شروع کنیم نه با دستگاه‌های مختصات یا چارچوب های مرجع. دوم آنکه دردسر زیادی کشیدیم تا سرعت های مطلق را از مکانیک نیوتنی حذف کنیم و بسیار خشنود بودیم که در فضا-زمان گالیله‌ای هیچ چیز سرعت مطلق ندارد. پس وقتی به عقب برمیگردیم تا نسبیت خاص را بر ادعاهایی درباره‌ی هر چیزی بنا کنیم باید این مسئله را به خاطر داشته باشیم. وقتی توضیح نسبیت مبتنی بر سخن گفتن از سرعت ها باشد، ناگزیر دوباره با فضا زمان و حرکت مطلق نیوتنی سر و کار خواهیم داشت. همیشه، نسبیت به نحوی ارائه شده که از این بیان ضمنی سوء استفاده شده است. مثلا میگویند «در نسبیت وقتی یک شیء سریع حرکت می کند زمان کند پیش می رود» یا «در نسبیت وقتی سرعت شیء به سرعت نور نزدیک می شود، شیء منقبض می شود» یا «در زندگی روزمره متوجه آثار مربوط به نسبیت نمی‌شویم زیرا با سرعتی نزدیک به سرعت نور به هیچ جا سفر نمی کنیم». هر یک از این ادعاها بیان می کند که یک جسم در هر لحظه مفروض، سرعتی دارد که می تواند به سرعت نور نزدیک تر یا از آن دورتر باشد. اما در نسبیت درست مثل فضا- زمان گالیله‌ای هرگز چنین سرعت هایی وجود ندارد. این که زمین اینک با چه سرعتی در حال حرکت است هیچ واقعیت فیزیکی ای ندارد؛ و نیز گفتن اینکه زمین با سرعتی نزدیک به سرعت نور حرکت نمی کند یا این که سرعت گردش زمین ۹۹ درصد سرعت نور است درست نیست. برای درک نسبیت باید تمام تصوراتمان را از چیزهایی که سرعت دارند، از جمله نور، از یاد ببریم.

با در نظر گرفتن ساختار هندسی فضا-زمان مینکوفسکی، قانون لختی نسبیتی پیشاپیش امکان پیش بینی هایی را برای ما فراهم می کند. مثلا، اگر مسیرهای دو موجود فیزیکی آزاد (اجسام غول آسا یا پرتوهای نور) یکدیگر را قطع کنند، آنها فقط یک بار همدیگر را قطع می کنند. زیرا در فضا-زمان مینکوفسکی، هیچ دو خط راستی بیش از یک بار همدیگر را قطع نمی کنند. این پیش بینی ممکن است تا حدی پیش پا افتاده به نظر آید اما بعدا خواهیم دید که در نسبیت عام این طور نیست.

برای آنکه پیش بینی های فیزیکی چشمگیرتری از این نظریه به دست آوریم، باید به ارتباط های بیشتر میان هندسه فضا-زمان مینکوفسکی و رفتار مشاهده پذیر اشیای مادی پی ببریم. مهم ترین این ارتباطات قضیه ای است که جایگاه نهایی آن را بعدا به دقت بررسی خواهیم کرد:

فرضیه ساعت: مقدار زمان سپری شده بین دو رویداد که یک ساعت دقیق نشان می دهد متناسب با بازه ای است که در امتداد مسیر ساعت میان آن رویدادهاست، یا، به طور خلاصه، ساعت ها بازه ای را که در امتداد مسیرشان است اندازه گیری می کنند.

فرضیه ساعت کلید فهم تمام مسائل مربوط به نسبیت را به دست می دهد.

تصور یک «ساعت» در نسبیت باید کمی معما گونه باشد. همه چیز به کنار، هنگام بنا کردن فضا- زمان مینکوفسکی هیچ جا چیزی شبیه به زمان مطلق نیوتنی را مفروض نگرفتیم. برخلاف فضا-زمان گالیله‌ای، فضا-زمان مینکوفسکی به برش های همزمان لایه لایه نمی شود؛ در واقع، حتی تصور «رویدادهای همزمان» اصلا هیچ معنایی ندارد. ساختار مخروط نوری تا حدی جایگزین لایه لایه شدن می شود. چون در نسبیت هیچ زمان مطلقی وجود ندارد، به یقین، ساعت ها نمی توانند آن را اندازه گیری کنند. اما ساعت ها باید چیزی را اندازه گیری کنند. دو ساعت دقیق که کنار یکدیگر قرار داده شوند، با هم تیک تیک می کنند، پس سازمان باید نوعی ساختار هندسی داشته باشد که هر دو ساعت آن را نشان دهند. بر اساس فرضیه ساعت، آن ساختار بازه است. در نسبیت ساعت های دقیق مانند کیلومتر شمارهای اتومبیل ها هستند که طول مسیرشان در خلال فضا-زمان را اندازه گیری می کنند. اگر این را بپذیریم، پس ساعت هایی که کنار یکدیگرند باید با هم تیک تیک کنند، زیر مسیر شان در فضا- زمان طول یکسانی دارد. اما ساعت هایی که از هر جدا و در مسیرهای مختلف باشند، زمان سپری شده بین یک جفت بازه همانند را کاملا متفاوت ثبت می کنند، درست مانند اتومبیل هایی که با انتخاب مسیرهای متفاوت برای رسیدن به یک موقعیت، کیلومتر شمارهای آنها مسافت های متفاوتی را نشان می دهند.

 

پارادوکس دوقلوها

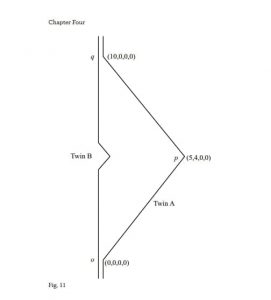
بیایید فرضیه ساعت را برای تبیین پدیده تمثیلی نسبیت، یعنی پارادوکس دوقلوهای معروف، به کار بریم. از نظر کیفی موقعیت از این قرار است: دو دوقلو، با ساعت هایی که عینا مثل هم ساخته شده اند، در آغاز کنار یکدیگر در سفینه های فضایی هستند و تحت تأثیر هیچ نیرویی نیستند. دو قلوی A لحظه ای موتورهایش را روشن و سپس خاموش می کند. دو قلوها از هم جدا می شوند. بعد از مدتی دو قلوی A دوباره موتورهایش را این بار در جهت مخالف روشن می کند. سرانجام او به عقب، به طرف دو قلوی B که هرگز موتورهایش را روشن نکرده است، رانده می شود. دو قلوی A موتورهایش را برای بار سوم روشن می کند و نسبت به دو قلوی B به حالت سکون نسبی برمی گردد. وقتی دو قلوها ساعت هایشان را مقایسه می کنند، می فهمند که ساعت دوقلوی B نسبت به A زمان بیشتری منحرف شده است. به علاوه، دوقلوی B از نظر بیولوژیکی پیرتر از دو قلوی A به نظر می رسد. نسبیت خاص این مسئله را چگونه پیش بینی می کند؟

بیایید چند ابهام را روشن کنیم.

ابهام ۱: در نسبیت، هر حرکتی، حرکت نسبی اجسام است. اما حرکت نسبی A نسبت به B دقیقا مانند حرکت نسبی B نسبت به Aاست. پس موقعیت فیزیکی آنها دقیقا یکسان است. پس بر اساس تقارن، وقتی آن دو به یکدیگر می رسند، ساعت هایشان باید زمان یکسانی را نشان بدهد.

ادعاهای ابهام ۱ نادرست هستند. ابتدا، این تعبیر که «در نسبیت هم حرکت ها نسبی هستند» به هیچ معنای جالب توجهی درست نیست. مثلا تبیین گوی های چرخان نیوتن در نسبیت خاص، اساسا با تبیینی که خود نیوتن ارائه داده است یا با تبیینی که در فضا-زمان گالیله‌ای ارائه شده است، یکسان است؛ فضا-زمان یک ساختار هندسی عینی دارد که مسیرهای لختی همه اجسام را، صرف نظر از هر جسم دیگری که وجود دارد، مشخص می کند. کشش ریسمان در هر حالت نشان می دهد که گوی‌ها مسیرهای لختی را دنبال نمی کنند، زیرا جهان‌خط‌های آنها منحنی هستند. نمودار فضا-زمان گوی‌های چرخان در نسبیت خاص درست مانند شکل زیر است بجز آن که به جای برش‌های همزمان، ساختار مخروط نوری خواهیم داشت. نسبیت یک نظریه فضا-زمان «نسبی گرایانه» از آن نوع که لایب نیتس به دنبال آن بود، نیست.

ابهام ۲: در بسیاری از کتاب‌ها «راه حل» پیشنهادی برای برطرف کردن پارادوکس دو قلوها، «شتاب» است؛ موقعیت دو قلوی A واقعا با موقعیت دو قلوی B متقارن نیست، زیرا دوقلوی A مجبور به استفاده از موشک‌هایش بود. موشک ها ( مطابق با قرائت نسبیت گرایانه قانون دوم نیوتن) نیرویی به وجود می آورند که دو قلوی A می تواند آن را احساس کند و این نیرو جهان‌خط او را خمیده می کند. دو قلوی B موشک‌هایش را استفاده نمی‌کند و هیچ نیرویی احساس نمی‌کند. پس دوقلوی B می‌داند که اوست که «واقعا ساکن است». و حال آن که دوقلوی او که نیرو را احساس می‌کند می‌داند که او «واقعا در حال حرکت است».

در این «تبیین» همه چیز اشتباه است.

ابتدا، توجه کنید که توانستیم این اثر را بدون محاسبه شتاب هر چین پیش بینی کنیم؛ ما فقط نسبت طول دو مسیر را محاسبه کردیم. شتاب ها هیچ نقشی در تبیین نتیجه نهایی ندارند. در واقع، به سادگی می توان موقعیت را تغییر داد به طوری که B دقیقا به اندازه A یا بیشتر از آن شتاب داده شود، اما در نهایت، باز هم B پیرتر از A باشد. در شکل زیر دقیقه همان شتاب ها را به مسیر B اضافه کرده ایم. اینک B دقیقا مانند A موتورهایش را روشن می کند، اما «تکان» کوچکی در جهان خط او، آن را به طرز چشمگیری کوتاه نخواهد کرد؛ پس وقتی یکدیگر را ملاقات می کنند هنوز هم او پیرتر است. اگر این تکان ها را افزایش دهیم، می توانیم به طور دلخواهی B را بیشتر از A شتاب دهیم و هنوز هم B پیرتر باشد.

در فضا-زمان مینکوفسکی برای آنکه دوقلوها به سمت یکدیگر برگردند حداقل باید یکی از آنها شتاب پیدا کند، زیرا، همان طور که قبلا گفتیم، یک جفت خط راست در فضا-زمان مینکوفسکی حداکثر یک بار می توانند یکدیگر را قطع کنند. این لازمه پارادوکس دوقلوهاست. در نسبیت عام، دو قلوهایی که هر دو همواره مسیرهای لختی دارند می توانند یکدیگر را بیش از یک بار ملاقات کنند و وقتی یکدیگر را ملاقات می کنند سن های متفاوتی داشته باشند. فاینمن و ریندلر، هر دو خاطرنشان می کنند که در نسبیت هم مانند فضا و زمان مطلق نیوتنی و فضا-زمان گالیله‌ای شتاب عینی است. این درست اما بی‌ربط است، زیرا مسئله این است که جهان خط‌ها چقدر طویل هستند نه اینکه چقدر خمیده هستند.

ابهام ۳: رابطه میان پارادوکس دوقلوها با «اتساع زمان نسبیتی» را بیان می کند و به عنوان این تز به تصویر کشیده می شود که «ساعتی که سریعتر حرکت می کند، آهسته تر تیک تیک می کند. اگر به این تز اضافه کنیم که دو قلوی A است که واقعا در حال حرکت است» و دو قلوی B «واقعا ساکن است»، در این صورت، دچار بدفهمی بزرگی شده ایم. پدیده دو قلوها یک مسئله ساده مربوط به هندسه فضا-زمان است، که بدون نسبت دادن هیچ نوع «حرکت» یا «سرعت» یا «سکون» به هیچ یک از آن‌ها، می توان آن را تبیین کرد. در فضا-زمان مینکوفسکی مانند فضا-زمان گالیله‌ای (و برخلاف فضا و زمان مطلق نیوتنی) در مقابل حرکت از هیچ مفهومی از «سکون» حمایت نمی کند. مسیر یک جسم می‌تواند مستقیم یا منحنی و بنابراین لخت یا شتابدار باشد، اما هیچ واقعیتی درباره آنکه «یک ساعت با چه سرعتی در حال حرکت است» به ما نمی گوید. یک دلیل قوی‌تر آن است که پارادوکس دوقلوها را نمی توان با استناد به این که هر یک از دوقلوها با چه سرعتی حرکت می کند، توضیح داد.
قانون نور، قانون لختی نسبیتی و فرضیه ساعت، رابطه میان رفتار امور مشهود و هندسه فضا-زمان مینکوفسکی را بیان می کند. برای تکامل دینامیک نسبیتی، به قرائتی از قانون دوم نیاز داریم که رابطه‌ی میان نیروی وارد بر یک شی را با انحنای جهان‌خط آن بیان کند. این امر مستلزم محاسبت عددی بیشتری است که نمی‌توانیم از عهده‌ی ورود به آن بر آییم. اما این سه اصل به تنهایی برای بیان ارتباط بین هندسه فضا-زمان مینکوفسکی با پدیده های مشاهده پذیر کفایت می‌کنند.

 

---

 

نسبیت خاص اساسا یک اصل مسلم درباره ساختار فضا-زمان است. اما چون هندسه فضا- زمان مستقیما ملموس نیست، رابطه این اصل با پیش بینی های تجربی فقط از طریق قوانینی است که رفتار اشیای ملموس را بیان می کنند. به طور مشابه، ساختار فضای اقلیدسی مفروض فقط وقتی می تواند در تبیین خواص نمودارهای مشاهده پذیر نقشی داشته باشد که ابزارهایی که نمودارها را ترسیم می کنند (راست لبه و پرگار) هندسه زیربنایی خود فضا را منعکس و از همین رو آشکار کنند. اگر این شباهت را در فضا-زمان مینکوفسکی آشکار کنیم، ماهیت آن شهودی تر می شود.

معادل پرگار اقلیدسی در مینکوفسکی، یک نظام فیزیکی است که همه رویدادهایی را که در بازه یکسانی در امتداد یک خط راست) از رویداد مرکزی قرار می گیرند متمایز می کند. در صورتی می توان از این الزامات تبعیت کرد که فرضیه ساعت را بپذیریم. فرض کنید مجموعه بزرگی از ساعت های زنگدار همسان داریم و همه طوری تنظیم شده اند که یک دقیقه پس از فشردن دکمه از کار بیفتند. در یک لحظه مشخص، دکمه فشرده می شود و ساعت ها از یک رویداد مرکزی (رویداد o در شکل زیر) با ضربه های کاملا متفاوتی در همه جهت ها فرستاده می شوند و مسیرشان را به صورت لختی ادامه می دهند.

 

اولین کار [برای بناکردن مختصات لورنتس] اختصاص یک مختصه t به هر رویداد است. فرض می کنیم که مجموعه نامحدودی از ساعت های آرمانی داریم و فرض می کنیم که می توانیم بگوییم یک ساعت تحت تأثیر هیچ نیروی خارجی ای نیست. این ساعت ها مطابق قانون لختی نسبیتی، مسیرهای زمان گونه مستقیمی را اشغال می کنند. به طور دلخواه یکی از این ساعت ها را «ساعت معیار» دستگاه مختصات انتخاب می کنیم. این انتخاب دلخواه، بسیاری از ویژگی های مهم مختصات حاصل را تعیین می کند. یک مقیاس زمانی دلخواه (مثلا ثانیه) و یک زمان صفر دلخواه برای ساعت معیار انتخاب می کنیم. با این مفروضات، ساعت معیار به هر رویداد روی جهان خطش ایک مختصه t اختصاص می دهد.

اتساع مختصه t به رویدادهای دور از مسیر ساعت معیار مستلزم استفاده از ابزارهای دیگر از جمله ساعت های دیگر است. اما در نحوه استفاده از این ابزارها باید محتاط باشیم. با توجه به رفتار پارادوکس دوقلوها، نمی توانیم به راحتی ساعت های کمکی را با ساعت معیار هماهنگ کنیم و سپس آنها را در فضا مستقر کنیم زیرا مسیرهای معینی که آنها از ساعت معیار به نواحی دورتر طی می کنند، روی قرائت آنها تاثیر می گذارد. بنابراین فرض می کنیم که این ساعت ها در تمام مسیرهای زمان گونه مستقیم در فضا-زمان مینکوفسکی وجود دارند و شروع به شناسایی مجموعه ای از ساعت های همگام میکنیم.

از نظر شهودی دو ساعت همگام دو ساعتی هستند که مسیر هر دو لخت باشد و نه به یکدیگر نزدیک و نه از یکدیگر دور شوند. لختی مسیر حائز اهمیت است، زیرا ساعت هایی که حول یک مرکز مشترک می چرخند ممکن است فاصله ثابتی را از یکدیگر حفظ کنند، اما نمی توان آنها را همگام در نظر گرفت. حتی به طور تحلیلی یا مفهومی نمی توان تضمین کرد که ساعت های همگام وجود داشته باشند، زیرا در برخی از فضا-زمانها هیچ دو مسیر لختی فاصله ثابتی را از یکدیگر حفظ نمی کنند. اما تقارنهای فضا-زمان مینکوفسکی ساختاری غنی از ساعت های همگام را امکان‌پذیر می‌کند.

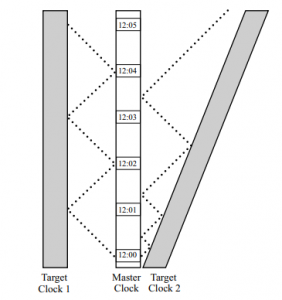
ناظر واقع در موقعیت ساعت معیار می تواند یک ساعت لخت همگام را با تنظیم راداری تشخیص دهد، بدین طریق که پرتوهای نور را از ساعت معیار به بیرون می‌فرستد و سپس یادداشت می‌کند که (بر اساس ساعت معیار) چقدر طول می‌کشد پرتوهای نور از ساعت هدف منعکس شوند و برگردند. ترسیم پرتوهای نور در نمودارهای‌مان ساده است زیرا مسیر نور در خلأ همیشه با یک خط راست با زاویه ۴۵ درجه نمایش داده می‌شود. اگر ساعت هدف با ساعت معیار همگام باشد، زمان رفت و برگشت نور همیشه یکسان است؛ اگر حرکت ساعت هدف نسبی باشد، زمان های رفت و برگشت تغییر می‌کنند (شکل زیر). برای آنکه نمودارهای فضا-زمان ما واضح‌تر باشند فقط نمودارهای فضا-زمان دوبعدی را ترسیم می‌کنیم اما این تکنیک را در هر جهتی می‌توان به کار برد.

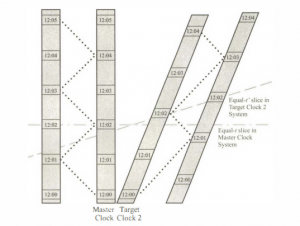
با این ابزار، ناظر واقع در موقعیت ساعت معیار می‌تواند ساعت های همگام را تشخیص دهد. ساعت هدف ۱ با ساعت معیار همگام است زیرا رفت و برگشت نور ۲ دقیقه طول می‌کشد. ولی برخلاف آن، ساعت هدف ۲ همگام نیست زیرا اولین رفت و برگشت کمتر از ۱ دقیقه و بعدی بیش از ۱ دقیقه طول می کشد. در فضا-زمان مینکوفسکی مجموعه کاملی از ساعت های همگام تمام فضا-زمان را پر می کند و آن را به مجموعه مسیرهای زمان گونه مستقیم موازی تقسیم بندی می کند. در هر رویداد دقیقا یکی از این ساعت ها وجود دارد و هدف ما به دست آوردن مختصه t رویداد است که از روی ساعت مناسب خوانده شده است. اما قبل از انجام این کار، باید ساعت های همگام را کالیبره و همزمان کنیم. کالیبراسیون، که انتخاب یک واحد اندازه‌گیری است، ساده است. فرض کنید ساعت معیار در هر دقیقه یک پالس نوری گسیل می کند و بنابراین اجازه می دهد که ساعت های هم‌گام واحد اندازه گیری‌شان را میزان کنند، طوری که بین سیگنال‌های پی‌درپی دریافتی یک واحد زمان سپری شود. این همه ساعت ها با «آهنگ یکسان» در حال تیک تیک‌کردن هستند.

در مرحله پایانی همزمان‌سازی باید بیشترین توجه صورت گیرد. در یک فضا-زمان کلاسیک مثلا فضا- زمان گالیله‌ای مفهوم همزمانی ساعت ها روشن است: همه ساعت ها زمانی واحد را به رویدادهای واقع در یک برش همزمان نسبت می دهند. چون در فضا-زمان کلاسیک این که کدام رویدادها با هم رخ داده‌اند یک واقعیت فیزیکی عینی دارد (یعنی در یک لحظه از زمان مطلق)، میزان کردن ساعت‌ها با معناست به طوری که آنها به رویدادهای هم‌زمان مختصه زمانی یکسان نسبت می‌دهند. اما در فضا-زمان مینکوفسکی، چنین ساختار همزمانی عینی‌ای وجود ندارد که ساعت‌ها به آن عکس العمل نشان دهند. اصلا هیچ واقعیت فیزیکی‌ای وجود ندارد در این‌باره که آیا این دو رویداد فضاگونه مجزا (یعنی رویدادهای خارج از مخروط های نوری یکدیگر) «در یک لحظه اتفاق افتاده‌اند». با این تعبیر، در نسبیت برای هم‌زمان سازی ساعت‌ها باید قراردادی وضع کرد.
این واقعیت که برش‌های tثابت و t’ ثابت با هم فرق دارند، به نسبیت هم‌زمانی(relativity of simultaneity) معروف است. مرسوم است که می‌گویند در نسبیت مفهوم هم‌زمانی برای یک ناظر یا یک حالت حرکت نسبی است. خواهیم دید که این توصیف، کمی درست است اما شاید به همان اندازه که خوب است، مضر هم باشد. ادعای کلیدی نسبیت آن است که همزمانی به عنوان یک رابطه فیزیکی واقعی بین رویدادها وجود ندارد. به علاوه، «نسبیت هم‌زمانی» بسیار برگرفته از چگونگی مختصات معیار است. در دستگاه‌های مختصات متفاوت مختصه های t متفاوت است و صفحه‌های مقادیر t ثابت آن‌ها فرق می‌کند. مختصات لورنتس فقط زیر مجموعه‌ای خاص از همه دستگاه‌های مختصات ممکن است که با تعریف معینی در فضا-زمان مینکوفسکی تشخیص داده می‌شود. اما در نسبیت عام، خواهیم دید که به طور کلی، مختصات لورنتس وجود ندارد و روندهای عملی فوق نمی‌توانند هیچ دستگاه مختصاتی را تعریف کنند. (همان طور که گفته شد، در نسبیت عام به طور کلی ساعت های لخت همگام وجود ندارد، بنابراین روش ما در مرحله اول با شکست روبه رو می‌شود.) برعکس، پدیده دو قلوها اثر فیزیکی ساده‌ای است که می توان آن را بدون استفاده از هر دستگاه مختصاتی توصیف کرد و در نسبیت عام نیز هم‌چنان وجود دارد.

در این جا بهتر است که شرایط منطقی را روشن کنیم. ابتدا که مفهوم دستگاه مختصات لورنتس را مطرح کردیم، کاملا بی‌ربط به فرایندهای فیزیکی بود و مختصات صرفا روشی انتزاعی برای مشخص کردن هندسه ذاتی فضا-زمان مینکوفسکی بود. سپس این هندسه را با مجموعه اصول فیزیکی قانون نور، قانون لختی نسبیتی و فرضیه ساعت به رفتار ماده ربط دادیم. سرانجام نشان دادیم که اگر این اصول پذیرفته شوند، با فرایند فیزیکی معینی، یعنی با استفاده از حرکت لختی ساعت‌های آرمانی و پرتوهای نور در خلأ، می‌توان مختصات لورنتس را برای فضا۔ زمان مینکوفسکی به دست آورد. در هیچ مرحله‌ای از این فرایند به «سرعت نور» یا اصل «سرعت ثابت نور است» اشاره نکردیم: در فضا- زمان مینکوفسکی به هیچ وجه امکان اندازه‌گیری عینی سرعت چیزی وجود ندارد. ما هیچ جا به مفهوم یک «دستگاه مختصات لخت» یا اصل «همه دستگاه های لخت هم‌ارزند» یا این که «قوانین فیزیک در همه دستگاه‌های لخت شکل یکسانی دارند» استناد نکردیم. بلکه یک ساختار هندسی معین برای فضا- زمان را اصل قرار دادیم، با برخی از اصول فیزیکی مفهوم فیزیکی آن ساختار را برای رفتار ماده قابل رؤیت بررسی کردیم و سپس شرح دادیم که چگونه از این مطلب برای بنا کردن دستگاه مختصات استفاده کنیم.
پس از انجام دادن همه این کارها، اینک می‌توانیم بفهمیم که معنی ثابت بودن «سرعت نور» و «دستگاه مختصات لخت» و «هم ارزی همه دستگاه های لخت» چیست.

نور، فی نفسه، سرعت ندارد، چون هیچ زمان مطلق یا مکان مطلقی در نسبیت وجود ندارد. اما، نسبت به یک دستگاه مختصات ، می توان برای پرتو نور یک سرعت مختصه در نظر گرفت. مثلا، در شکل بالا پرتو نوری که از ساعت معیار به ساعت هم‌گام می رسد چقدر «سریع» می رود؟ خب، در دستگاه مختصات بدون پریم، مقدار ا پرتو نور گسیل شده از ساعت معیار ۱۲:۰۰ است و وقتی به ساعت هم‌گام می رسد ۱۲:۰۱ است، بنابراین اختلاف مقادیر t («زمان سپری شده» در این دستگاه مختصات) ۱ دقیقه است. توجه کنید که «زمان سپری شده» با هیچ ساعت خاصی اندازه‌گیری نشده است، بلکه به فرایندهای ما برای تنظیم ساعت‌های هم‌گام بستگی دارد. پس در این مختصات وابسته ۱ دقیقه طول می‌کشد تا پرتو از ساعت معیار به ساعت هم‌گام برود. پرتو نور در این سفر چه «مسافتی» طی کرده است؟ دوباره هیچ جواب عینی‌ای برای این سؤال وجود ندارد زیرا چیزی شبیه پایندگی فضای مطلق نیوتن نداریم. اما مختصه ساعت هم‌گام در دستگاه مختصات ساعت معیار ۱- است و مختصه های yو zآن صفرند. پس (با استفاده از معادله فیثاغورس) می توان گفت که ساعت همگام ۱ دقیقه نوری طی کرده است. پرتو نور (در این مختصات) ۱ دقیقه نوری را در ۱ دقیقه (در این مختصات) طی می کند، پس سرعت مختصه آن در این دستگاه مرجع ۱ دقیقه نوری در دقیقه است.

اینک ممکن است تمام این محاسبات در نظر خواننده تقلب محسوب شود. با توجه به تعریفی که برای مختصات ارائه دادیم، بدیهی است که «سرعت مختصه» نور ۱ دقیقه نوری در دقیقه است. اگر زمان بر حسب دقیقه و فاصله ها بر حسب دقیقه نوری باشد، پس بنا به تعریف یک پرتو ۱ دقیقه نوری در ۱ دقیقه طی می کند. با این تعبیر، چون این نتیجه قبلا در فرایند تعیین مختصات به کار برده شده است، پس این محاسبات تقلب است. اما این نتیجه‌ای ناخوشایند نیست. سعی کرده ایم فضا و زمان مطلق نیوتنی را کنار بگذاریم، پس سرعت های مطلق نیوتنی نیز باید کنار گذاشته شود و این امر برای نور نیز مانند هر چیز دیگری اعتبار دارد. با این تعبیر، «ثابت بودن سرعت نور» نمی‌تواند یک اصل فیزیکی بنیادین باشد.

اما نباید در جهت دیگر زیاده‌روی کنیم. سرعت مختصه نور در تمام دستگاه‌های مختصات لورنتس ثابت است ولی در دستگاه‌های مختصات دیگری، که می توان در فضا-زمان مینکوفسکی تعریف کرد، ثابت نیست. (مثلا، فقط مختصه t یک دستگاه لورنتس را با مختصات x، y و z دستگاه دیگری ترکیب کنید.) اما این واقعیت که مختصات لورنتس و رابطه آنها با رفتار نور و ساعت ها، امکان‌پذیر است به هیچ وجه قراردادی نیست. این واقعیت که تمام نورهای گسیل‌شده از یک رویداد (در خلا) در امتداد مخروط نوری منتشر می‌شوند قراردادی نیست. وجود داشتن ساعت‌های هم‌گامی که تعریف کردیم، قراردادی نیست. اصل موضوع فضا-زمان مینکوفسکی یک تز فیزیکی است نه یک قرارداد.
وقتی درباره‌ی «چارچوب مرجع ساعت» صحبت می‌کنیم، منظورمان مجموعه مختصات لورنتسی است که در آن مختصه سرعت ساعت صفر است. در چنین چارچوب مرجعی، وقتی می‌گوییم اشیا «چگونه دیده می شوند» منظورمان فقط این است که مختصات رویدادها در آن دستگاه چیست اند. این موضوع نباید با «ناظر اشیا را چگونه می‌بیند» اشتباه گرفته شود که مفهوم بسیار متفاوتی دارد و به معنی آن چیزی است که اگر ناظر چشمان‌ش را باز کند، عینا خواهد دید. آنچه ناظر میبیند توسط نوری که از مردمک‌هایش می‌آید تعیین می‌شود و اصلا هیچ ربطی به مختصات و دستگاه مرجع ندارد.

مثلا، اتساع زمانی مختصات معیار بیان می‌کند که چگونه مختصات لورنتس، که با ناظر متحرک لخت همراه است، وابسته به ساعتی است که نسبت به ناظر حرکت می‌کند. با این بیان، یک ساعت متحرک «همیشه به نظر» ناظر به آرامی تیک تیک می‌کند. اما اگر ناظر با یک تلسکوپ ساعت را مشاهده کند، عینا چنین چیزی را نمی‌بیند. با این بیان، مشاهده به معنای واقعی (نه به معنای اطلاق مختصات) نشان می‌دهد که ساعت گاهی اوقات کند و گاهی اوقات سریع حرکت می کند. اگر به سناریوی دوقلوها برگردیم، به سادگی با افزودن پرتوهای نور به نمودار، بدون استفاده از هر مختصاتی، می توانیم تعیین کنیم که هر دوقلو عینا چه می‌بینند. برای ساده‌کردن مسئله فرض کنید که هر یک از دو قلوها با توجه به ساعتش هر ۱۰ روز که سپری شود، یک پالس نوری به بیرون می‌فرستد.

اگر منظورمان از «به نظر رسیدن» نمود بصری واقعی چیزی برای ناظر باشد، هیچ قانون کلی‌ای وجود ندارد که نشان دهد ساعت با چه سرعتی تیک تیک می‌کند. می‌توان این نمودها را با بررسی نمودار فضا-زمان معلوم کرد و اصلا هیچ نیازی به استفاده از هیچ‌گونه دستگاه مختصاتی نیست. این یک مسئله فیزیکی است و ابداع مختصات فقط برای راحتی محاسبات است.

‌

فرضیه ساعت

برای آنکه هندسه فضا-زمان را به رفتار مشاهده پذیر امور ملموس ربط دهیم، به چند اصل فیزیکی نیاز داریم. در فصل قبل هندسه فضا-زمان را هندسه مینکوفسکی فرض کردیم و با توجه به قانون نور، قانون لختی نسبیتی و فرضیه ساعت، برخی از نتایج مشاهده پذیر آن را بررسی کردیم. به علاوه فرض کردیم که توانستیم تعیین کنیم که جسم تحت تأثیر هیچ نیروی خارجی ای نیست و ناحیه خاصی از فضا-زمان خلا است. با این فرض ها، پدیده دو قلوها را استنتاج کردیم و نشان دادیم که چگونه می توان ا مختصات لورنتس را از نظر فیزیکی و بصری در فضا-زمان بنا کرد.

از میان سه اصل فیزیکی نام برده شده، فرضیه ساعت موردی خاص است. قانون نور و قانون لختی نسبیتی شرح می دهند که پرتوهای نور و اجسام غول آسایی که تحت تأثیر نیرو نیستند، در فضا – زمان مینکوفسکی چگونه رفتار می‌کنند و این دو اصل با آن نوع واژه‌هایی بیان می‌شوند که در هر قانون فیزیکی انتظار داریم. اما فرضیه ساعت در کل متفاوت است، زیرا این فرضیه بیان می کند که ساعت ها (با توجه به هندسه مینکوفسکی) چگونه رفتار می کنند، اما واضح است که «ساعت» آن نوع اصطلاحی نیست که باید در بیان یک قانون فیزیکی بنیادین به کار رود. طبیعت می تواند میان نور و ذرات بزرگ تمایز قائل شود اما برای تعیین کردن نحوه رفتار یک ساز و کار مشخص مجبور نیست تعیین کند که آیا آن ساز و کار یک ساعت به حساب می آید یا نه. عبارتی مثل «ساعت»، برخلاف «پرتو نور» یا «ذره بزرگ»، در توضیح هیچ قانون فیزیکی بنیادینی دیده نمی شود.

اینشتین از این امر آگاه بود و تصدیق کرد که هر مبحثی از فیزیک که با عبارت هایی مثل «ساعت ها» یا «میله های اندازه گیری» بیان شود، فقط یک تدبیر موقتی است:
ابتدا، تذکری درباره نظریه (نسبیت خاص) که قبلا نیز بیان شد. (این واقعیت) به ذهن خطور می کند که نظریه ( بجز برای فضای چهاربعدی) دو نوع چیز فیزیکی را شرح می دهد: (۱) میله های اندازه گیری و ساعت‌ها، (۲) همه چیزهای دیگر مانند میدان الکترو مغناطیسی، نقطه مادی و الی آخر. این به معنای خاصی، ناسازگار است؛ به بیان دقیق میله های اندازه گیری و ساعتها وجودهای خودکفای نظری نیستند بلکه به عنوان راه حل های معادلات اصلی (اشیایی متشکل از پیکربندی های اتمی متحرک) ارائه می شوند. با وجود این، این فرایند خود را توجیه می کند، چون از همان آغاز واضح بود که اصول مسلم این نظریه آن قدر محکم نیستند که از آنها برای رخدادهای فیزیکی ای که به اندازه کافی غیردلبخواهی اند معادلاتی را استنتاج کرد که به قدر کفایت کامل باشند، تا نظریه میله های اندازه گیری و ساعت ها را بر مبنای این چنینی بنا کرد. اگر قرار بود که به طور کلی مختصات را از نظر فیزیکی تفسیر نکنیم (چیزی که به خودی خود امکانپذیر است)، بهتر بود این ناسازگاری را – هرچند باید در مرحله بعدی نظریه برطرف شود – نادیده بگیریم. اما نباید تا آن جا دچار اشتباه شویم که تصور کنیم بازه‌ها نوع خاصی از وجودهای فیزیکی هستند که ذاتا با متغیرهای فیزیکی دیگر فرق دارند… ( Einestein (1982) pp. 59_61)

ما فقط درباره ساعت ها و پرتوهای نور توضیح داده ایم و از اشاره کردن به «میله های اندازه گیری» اجتناب کرده ایم، اما مشکل ساعت ها به قوت خود باقی است و، همان طور که خواهیم دید، مسئله «میله های صلب» به زودی آشکار خواهد شد. پس، موقعیت دقیق فرضیه ساعت چیست و چگونه می توانیم درخواست اینشتین را اجابت کنیم که ساعت ها چیزی نیستند جز پیکربندی های اتمی متحرکی که از قوانین میدان های الکترومغناطیسی و ذرات مادی و الی آخر پیروی می کنند؟

اولین چیزی که باید توجه کرد آن است که خود عبارت «فرضیه ساعت» انتخاب خوبی نیست. این عبارتی است که در کتاب های فیزیک به کار می رود اما هیچ راهی برای بیان مضمون چنین فرضیه ای به روش عمومی وجود ندارد. ترجیحا باید به جای یک فرضیه با یک تعریف شروع کنیم…

تعریف ساعت: ساعت آرمانی نوعی وسیله فیزیکی مشاهده پذیر است که به رویدادهای روی جهان خطش عدد اختصاص می دهد، به طوری که نسبت اختلاف اعداد متناسب با نسبت طول پاره خط های روی بازه جهان خط است و رویدادها همان نقاط انتهایی پاره خط ها هستند.

ساعت نوری شامل یک پرتو نور است که بین دو آینه به عقب و جلو منعکس می شود. فرض می کنیم سازوکاری وجود دارد (و این جا دوباره از ارائه یک تحلیل فیزیکی کامل شانه خالی می کنیم) که می تواند پرتو نور رسیده به یکی از آینه ها را ثبت کند و وقتی این اتفاق افتاد «تیک تیک می کند». به علاوه فرض می کنیم سازوکاری هم شمار تیک ها را ثبت می کند. این وسیله بدین طریق به رویدادهای خاصی در امتداد جهان خطشان اعداد صحیحی نسبت می دهد. اینشتین در مباحثه اش به این نوع ساعت اشاره می کند:

(در اصل) پیش فرض وجود میله های اندازه گیری و ساعت های (آرمانی، یعنی بی نقص مستقل از یکدیگر نیستند، زیرا سیگنال نوری‌ای که بین دو انتهای یک میله صلب به عقب و جلو منعکس می شود، یک ساعت آرمانی تشکیل می دهد، به شرطی که اصل ثابت بودن سرعت نور در خلا منجر به تناقضات نشود.

اینشتین تصریح می کند که آینه ها باید به دو انتهای یک «میله صلب» چسبیده باشند، اما ما تاکنون مفهوم میل صلب را بیان نکرده ایم، خواهیم دید که بدون آن چقدر ممکن است گیج شویم.

دستگاهی را در نظر بگیرید که شامل دو آینه متحرک لخت در فضا-زمان مینکوفسکی است و مسیر حرکت آنها موازی است. یک پرتو نور متوالیه بین دو آینه منعکس می شود و شمارشگری تعداد دفعاتی را که پرتو نور به یکی از آینه ها می رسد ثبت می‌کند. مادامی که آینه ها تحت تاثیر نیرو نباشند، این دستگاه به مثابه یک ساعت آرمانی رفتار می کند.

«تیک های» متوالی پرتو نوری که به آینه برخورد می کند، جهان خط آینه را به پاره خط های مساوی تفکیک می کند. در اصل، در شکل بالا می‌توانیم آینه ها را جایگزین ساعت معیار و ساعت هدف ۱ کنیم، سپس پرتو نور رسیده به یکی از آینه ها را برای تعریف ساعت به کار بریم. در این جا برای ما مهم نیست که توضیح دهیم چطور می توان فهمید مسیر آینه ها نسبت به یکدیگر موازی است چون به سادگی آن را بخشی از مشخصات فیزیکی دستگاه مورد بحث در نظر میگیریم.

با تعریف ارائه شده قید دست و پاگیری روی این وسیله اعمال می شود، به طوری که فقط می توانیم ثابت کنیم مادامی که حرکت هر دو آینه لخت باشد این وسیله یک ساعت آرمانی خواهد بود. برای آن که دستگاهی یک ساعت آرمانی باشد، باید بدون اهمیت به آنکه چه نوع مسیری را دنبال می کند، به اندازه گیری بازه ادامه دهد. بیایید با سؤال ساده تری شروع کنیم. اگر این دستگاه را با شتابی ناگهانی در یک جهت، از یک حرکت لختی به حرکت لختی دیگری ببریم، دستگاه چگونه رفتار می کند؟ به طور خلاصه، اگر دستگاهمان را از حرکت لختی فعلی اش به حرکت دیگری ارتقا دهیم، چگونه رفتار می کند؟

توجه کنید که برهم‌کنش‌های فیزیکی‌ای که بررسی می‌کنیم صرفا از دید برخی از چارچوب های لورنتس، از جمله چارچوب لورنتس اولیه که در آن آینه‌ها ساکن هستند، به درستی به عنوان انقباض فاصله میان آینه‌ها توصیف شده اند. در دیگر چارچوب های لورنتس همین تغییر، از دید آن‌ها انبساط فاصله بین آینه‌ها توصیف می شود. با این همه، باید دلیل فیزیکی محسوسی وجود داشته باشد که آینه‌ها چگونه عمل می‌کنند زیرا در این جا مسئله را به صورت فیزیکی بررسی می‌کنیم نه این که صرفا دستگاه‌های مختصات را آنالیز کنیم.

پیش از این دیدیم که به عقیده ریندلر انقباض لورنتس فیتزجرالد پیامد نیروهای فیزیکی نیست بلکه صرفا تصویری هندسی است. همان طور که جان استوارت بل شرح می دهد، فیزیک‌دان ها از این دیدگاه خیلی دفاع کرده اند. بل، که در شتاب دهنده ذره در سرن کار می‌کرد، نتیجه یک آزمایش غیررسمی را که وی مجری آن بود گزارش می‌دهد. او موقعیتی را که خیلی شبیه دو آینه ماست برای همکارش شرح داد: دو موشک عینا همسان حرکت لختی را شروع می‌کنند و در سکون متقابل هستند. یک سیگنال به بیرون فرستاده می شود، پس موتورهای موشک «در آن لحظه» در چارچوب سکون لورنتس‌شان شروع به کار می‌کنند. چون موشک‌ها همسان هستند مسیر آنها در نمودار فضا-زمان موازی و با فاصله برابر نشان داده می‌شود، بنابراین از دید چارچوب لورنتیس اول موشک‌ها مانند آینه‌های ما در شکل پایین، فاصله ای ثابت از یکدیگر را حفظ می‌کنند. بل سپس این نکته جزئی را اضافه کرد که ریسمان محکمی به انتهای دو موشک بسته و کشیده شده است. سپس بل از همکارانش، که از معتبرترین فیزیکدان های نظری و تجربی دنیا هستند، یک سؤال ساده فیزیکی کرد: آیا ریسمان پاره می شود؟

بل شرح می دهد:

این مسئله قدیمی زمانی در بوفه سرن مطرح شد. یک فیزیک‌دان برجسته تجربی نپذیرفت که ریسمان پاره خواهد شد و چون اصرار داشتم که ریسمان پاره می شود، آن را تصویر غلط شخصی از نسبیت خاص پنداشتند. تصمیم گرفتیم برای حل اختلاف به سرن متوسل شویم و یک تصویر (نه خیلی سیستماتیک) از این موضوع ترسیم کنیم. نتیجه آرای عمومی این بود که ریسمان پاره نمی‌شود. (Bell (2008) p. 68)

اما در واقع همان طور که در شکل پایین نشان داده شده است، ریسمان پاره می‌شود.

فیزیک‌دان های سرن هم حتما مانند ریندلر فکر می‌کردند زیرا اگر انقباض لورنتس فیتزجرالد صرف مربوط به نگاه کردن به رویدادهای یکسان از زاویه متفاوت بود یا صرفا مربوط به توصیف رویدادهای یکسان در دستگاه مختصات متفاوت بود، آن وقت بدیهی بود که این امر موجب پاره شدن ریسمان نشود! اگر این امر واقعا به نیرویهای الکتریکی یا بین اتمی ربطی نداشته باشد، پس هیچ پیامد فیزیکی مشاهده‌پذیری نمی تواند داشته باشد و در واقع آنچه انقباض مختصات معیار لورنتس – فیتزجرالد نامیده‌ایم چیزی بیش از مشاهده رابطه بین دستگاه های متفاوت مختصات لورنتس نیست. اما همان طور که بل به حق پافشاری می کند یک انقباض لورنتس – فیتزجرالد فیزیکی نیز وجود دارد که قطعا به نیروهای بین اتمی وابسته است و می تواند آثار فیزیکی داشته باشد. برای آن که بفهمیم چگونه یک ساعت آرمانی بسازیم، باید این اثر فیزیکی را درک کنیم.
در یک تحلیل کلی پاسخ در مفهوم جسم صلب نهفته است. اینشتین از «میله های اندازه گیری» اسم می برد و ویژگی اصلی میله های اندازه گیری آن است که، به تعبیری، صلب اند. اگر سعی کنیم یک میله صلب را در هم بفشاریم، در مقابل فشردگی مقاومت می کند و اگر سعی کنیم آن را بکشیم، نیز مقاومت می کند. یعنی جسم صلب حالت تعادل دارد طوری که تمایل دارد در برابر نیروهای خارجی (به قدر کافی کوچک) مقاومت کند و به حالتی برگردد که نیروهای خارجی وجود نداشتند. دستگاه دو آینه‌ای ساده ما بدون میله رابط یک دستگاه صلب نیست زیرا آینه‌ها تمایل ندارند در برابر نیروهای خارجی مقاومت کنند و در حالت تعادلی ثابتی باقی بمانند.

 

توصیفات عمیق تر اصول فیزیکی

برای استخراج پیش بینی های تجربی از روایت هندسه فضا-زمان به اصولی نیاز داریم که این هندسه را به رفتار مشاهده پذیر وجودهای فیزیکی ربط دهد. سه مورد از این اصول، یعنی قانون نور، قانون لختی نسبیتی و فرضیه ساعت را در مبحثمان به کار بردیم. دو اصل اول، برخلاف آخری، شکل درستی از قانون های بنیادین طبیعت هستند. اما آنها نیز باید پیامد قوانینی عمیق‌تر باشند که بر حسب مفاهیم متفاوت بیان شده‌اند.
مثلا، الکترودینامیک ماکسول را می توان بر حسب فضا-زمان مینکوفسکی فرموله کرد: به همین دلیل است که بررسی پدیده های الکترو مغناطیسی در وهله اول به نسبیت منتهی شد. بنابراین می‌توانستیم الکترودینامیک ماکسول را در حکم یک قانون فیزیکی نسبیتی بنیادین اصل موضوع قرار دهیم و سپس پرتوهای نور را همچون امواج الکترومغناطیس شناسایی کنیم و پس از آن استنتاج کنیم که مسیر یک پرتو نور در خلأ روی مخروط نوری قرار می گیرد، نه این که آن را یک اصل مسلم فرض کنیم.
برای قانون لختی نسبیتی نیز نکات مشابهی وجود دارد. قانون لختی نسبیتی تقلیدی از قانون اول حرکت نیوتن است و شکل درستی از یک قانون طبیعی بنیادین است. اما ممکن بود این طور نباشد. می توانستیم مسیرهای اجسام غول آسا را به نحوی توصیف کنیم که نتیجه‌اش این باشد که این اجسام همیشه، شاید فقط به طور تقریبی، وقتی تحت تأثیر نیروهای خارجی نباشند در امتداد خطوط راست در فضا-زمان پیش می‌روند. هرچه قوانین بنیادین بیشتری بر حسب هندسه مینکوفسکی بیان شوند، نسبیت خاص هم به همان اندازه تأیید خواهد شد. فقط سؤال اساسی این است که آیا ساختار فضا- زمان مینکوفسکی همه ساختار فضا- زمانی است که برای آموختن فیزیک لازم است و آیا پیش‌بینی‌های حاصل از قوانین فیزیکی‌ای که بر اساس آن ساختار بیان شده‌اند، دقیق خواهد بود. نظریه ماکسول نشان داد که چگونه توانستیم این کار را برای الکترو مغناطیس و پس از آن برای ادغام نیروهای هسته‌ای ضعیف و قوی انجام دهیم. اما تلاش برای ارائه فیزیک نسبیت خاص با مانع جاذبه روبه رو شد. ماحصل این مشکل نظریه نسبیت عام بود.

فضای خمیده و فضا-زمان خمیده نسبیت عام به مثابه نظریه ای در باب گرانش بسط یافت که روایت کیفی ساختار فضا-زمان مبتنی بر نسبیت خاص را شامل می شود. چند چیز موهوم درباره نسبیت عام رایج است که قبل از ارائه این نظریه ضروری است این ابهامات را رفع کنیم. اغلب میگویند نسبیت عام عمومیت بخشیدن به نسبیت خاصی است به طوری که در نسبیت خاص همه چارچوب های مرجع لخت (یعنی همه چارچوب های لورنتس) هم ارزند و در نسبیت عام همه چارچوب های مرجع هم ارزند؛ یا در نسبیت خاص تمایزی فیزیکی میان حرکت شتابدار و بدون شتاب وجود دارد اما در نسبیت عام وجود ندارد؛ یا در نسبیت خاص فضا-زمان ساختاری لخت دارد که تابعی از توزیع اجرام نیست اما در نسبیت عام تابعی از توزیع اجرام است (که ماخ از طرفداران آن بود). همه این ادعاها نادرست اند. نسبیت عام نیز دقیقا مانند نسبیت خاص یک ساختار هندسی ذاتی عینی به فضا-زمان نسبت می دهد و این ساختار هندسی ساختاری مستوی است که حرکت شتابدار را از حرکت بدون شتاب متمایز می کند. تبیین نسبیتی عام برای پدیده گوی های چرخان نیوتن دقیقا به همان فرم کلی تبیینی است که در نسبیت خاص یا، در واقع، در فضا-زمان گالیله‌ای ارائه شد: دقیقا وقتی گوی ها شتابدار (یعنی در حال چرخش) هستند در ریسمانی که آنها را به هم وصل می کند، کششی ایجاد می شود. این شتاب نسبت به ساختار ذاتی فضا-زمان تعریف می شود، زیرا ممکن است گوی‌ها تنها اشیای مادی موجود باشند. طبق نسبیت عام حقیقت دارد که توزیع ماده هندسه فضا- زمان را تحت تأثیر قرار می دهد، اما توزیع ماده هندسه فضا- زمان را تعیین نمی‌کند. مثلا، در نسبیت عام راه حل‌های خلا متمایز بسیاری وجود دارند که در هر یک از آنها فضا-زمان خالی از هر ماده و انرژی ای است. یکی از این راه حل های خلأ فضا-زمان مینکوفسکی است.

گاهی اوقات نیز می گویند یافتن یک نظریه گرانش نسبیتی چالش خاصی بود زیرا نیروی گرانشی نیوتنی آنی است، در حالی که در نسبیت دیگر هیچ مفهوم همزمانی ای وجود ندارد که بتوان با آن کنشی آنی را تعریف کرد. به چندین دلیل این تصور اشتباه است. اول آنکه احتمالش بسیار کم است که نیوتن واقعا تصور کرده باشد که نیروی گرانش آنی است، زیرا می‌دانست که در این نیرو باید نوعی ذره میانجی‌گری کند که زمانی طول می کشد تا، مثلا، از خورشید به زمین برسد. البته دقیقا اینجا بود که نیوتن اعلام کرد «من فرضیه نمی سازم». اما مهم تر آن که در شکل کلی قانون گرانشی نیوتن هیچ چیزی وجود ندارد که برای شکل نسبیتی آن مشکلی به وجود آورد، مثلا، قانون الکترواستاتیک کلمب درست مثل قانون گرانش نیوتن قانون نیروی عکس مربع است و این قانون در حالت حدی مناسب از الکترودینامیک مکسول به دست می آید. اما دینامیک مکسول کاملا نسبیتی است. در واقع، وقتی اینشتین نسبیت خاص را در سال ۱۹۰۵ مطرح کرد، هنوز زمان زیادی نگذشته بود که بسیاری از نظریه های نسبیتی خاص مختلف در باب گرانش توسعه یافت. خود اینشتین روی تعدادی از این نظریه ها کار کرد و آنها را رد کرد چون، همان طور که به زودی خواهیم دید، این نظریه ها [اقتضائات] اصل هم ارزی ضعیف یا اصل هم ارزی قوی را برآورده نمی کردند. فقط با نظریه عام در سال ۱۹۱۵ همه معیارهای اینشتین برآورده می شدند اما مبحث مهم این نظریه کنش آنی نبود.

 

تبیین هندسی در غیاب گرانش

اگر مهم ترین آزمایش در تاریخ فیزیک فضا-زمان آزمایش سطل نیوتون بود، پس از آن مهم ترین آزمایش را گالیله انجام داد. گالیله در مجله دو علم جدید ادعای ارسطو را که اجسام با سرعتی متناسب با وزنشان سقوط می کنند، رد می کند. چون اجسام سنگین تر نسبت به اجسام سبک تر نیروی گرانش بیشتری دارند بدیهی است انتظار داشته باشیم که اجسام سنگین تر سریع تر سقوط کنند اما گالیله اثبات کرد که اختلاف در سرعت نزول قابل چشم پوشی است.

نظریه گرانشی نیوتن بر اصل هم ارزی ضعیف دلالت دارد، زیرا تأکید می‌کند نیروی گرانشی که جسم احساس می کند متناسب با جرم آن است.

توصیف نیوتن جرم سه نقش فیزیکی مجزا دارد:

1. جرم اندازه گیری مقاومت طبیعی جسم در برابر نیرو برای شتاب گرفتن است (جرم اختی)
2. جرم اندازه گیری مقدار نیروی گرانشی است که یک جسم به اجسام دیگر وارد می کند (جرم گرانشی کنشگر)
3. جرم اندازه گیری میزان تأثیرپذیری یک جسم از نیروی گرانش اجسام دیگر است (جرم گرانشی کنش پذیر)

با این توصیف، اصل هم ارزی ضعیف تأکید می کند که جرم لختی یک جسم متناسب با جرم گرانشی کنش پذیر آن است. اگر چنین باشد، نیروهای گرانشی وارد بر دو جسم مورد آزمون متناسب با جرم لختی آنهاست، پس (اگر نیروها فقط گرانشی باشند) آنها شتاب یکسانی را تجربه می کنند. بنابراین گلوله توپ و ساچمه تفنگ فتیله ای با هم سقوط می کنند.

نیوتن اصل هم ارزی ضعیف را با استفاده از پاندولی که از مواد مختلف ساخته شده بود آزمود و دریافت که تا یک در چندین هزار اعتبار دارد. آزمایش های جدید تصدیق کرده اند که این اصل تا یک در ۱0۱۲ اعتبار دارد. از منظر نیوتنی، تبیین روشن اصل هم ارزی این است که جرم لختی همان جرم گرانشی کنش پذیر است، پس این تناسب باید دقیق باشد. به طور مبهمی اصل هم ارزی ضعیف جز گرانش برای نیروهای دیگر به هیچ وجه برقرار نیست. مثلا، دو ذره مورد آزمون که فقط تحت تأثیر نیروهای الکترومغناطیسی باشند، بسته به اینکه بار مخالف داشته باشند، یا یکی باردار و دیگری خنثی باشد، به روش های متفاوت شتاب می یابند. با این تعبیر، اصل هم ارزی ضعیف می گوید که هر جسم غول آسایی دقیقا به همین روش با گرانش جفت می شود، برخلاف نیروهای دیگر که تأثیرشان روی یک جسم بستگی به این دارد که آن جسم چگونه باردار شده باشد.
تبیین نیوتن از اصل هم ارزی ضعیف هیچ مشکل تجربی‌ای ندارد، با این همه، اینشتین ایراد مفهومی خاصی را در تبیین نیوتن کشف کرد. برای پی بردن به نارضایتی اینشتین به مشاهدات خود نیوتن بر می گردیم. آزمایش سطل و مثال گوی ها رابطه میان نیروی خالص وارد به یک جسم را با شتاب مطلق آن، یا به عبارتی انحنای جهان خط آن بیان میکند. منبع نیروهای وارد بر یک شیء را می توان مشاهده کرد، مثل [منبع] کشش ریسمان گوی ها. در واقع، یک روش برای ساختن شتاب سنج، آن است که منبع نیرو را نمایان کنیم. مثلا، یک وزنه ساده را در نظر بگیرید که آزادانه در لوله ای حرکت میکند و توسط فنرهایی به دو انتهای لوله می چسبد. اگر این دستگاه را در اتومبیلی قرار دهیم، طوری که لوله رو به جلو باشد و شتاب بگیریم، وزنه در لوله «به عقب برمیگردد». فنر جلویی کشیده و فنر عقبی فشرده می شود تا زمانی که فنرها بتوانند نیروی کافی به وزنه اعمال کنند تا وزنه همراه اتومبیل شتاب بگیرد. با فرض این که فقط فنرها یک نیروی رو به جلو به وزنه وارد کنند، فشردگی و کشش فنرها شتاب اتومبیل را اندازه می گیرد. این همان پدیده ای است که به ذهن کلارک خطور کرد، وقتی که از «شوکی» نوشت که یک جسم تجربه می کند تا از حالت حرکت یکنواخت مطلق به حالت سکون مطلق برسد؛ یعنی وقتی جسم شتاب می گیرد.

فرض کنید گالیله با این شتاب سنج که جهت پایین را نشان می دهد بالای برج ایستاده است. وزنه به طرف پایین لوله پرتاب می شود، پس فنر بالایی را کشیده و پایینی را فشرده می کند. به نظر نیوتن، این روش شتاب دستگاه را نشان نمی دهد، بلکه فنرها دقیقا نیروی کافی برای خنثی کردن گرانش را تأمین و بنابراین حرکت لختی وزنه را حفظ می کنند. چون برای عمل‌کرد مناسب شتاب‌سنج، فقط فنرها نیرویی موازی با لوله اعمال می کنند، پس گالیله این دستگاه را به درستی به کار نمی برده است. اگر گالیله شتاب سنج را رها کند تا سقوط کند، فنرها وزنه را به وضعیت خنثی بر می گردانند. چون روکش بدنه این دستگاه و وزنه داخل آن با آهنگ یکسان سقوط می کنند پس هیچ نیروی اضافه‌ای لازم نیست تا فنرها را کنار هم نگه دارد. سقوط شتاب سنج هیچ اثر قابل مشاهده ای از شتاب را نشان نمی دهد: شتاب سنج درست مانند وقتی عمل می‌کند که در فضای خالی بدون هیچ گرانشی حرکت لختی دارد. به نظر نیوتن، باز هم این استفاده ای نابجا از این دستگاه است.

برای دست یافتن به مفاهیم اصلی نسبیت عام، فقط باید این نمود را – ناتوانی شتاب سنج در حال سقوط برای ثبت هر شتابی – همان طور که هست بپذیریم. فرض کنید در شکل بالا به سادگی «نیروی گرانش» را از نمودار حذف کنیم. پس به گوی های در «حال سقوط» هیچ نیرویی وارد نمی شود و گالیله روی خودش نیرویی نامتعادل در خلاف جهت زمین احساس می کند. طبق قانون لختی فضا۔ زمان، اجسامی که تحت تأثیر هیچ نیرویی نباشند مسیرشان در فضا-زمان مستقیم است، پس مسیر گوی‌ها مستقیم و مسیر سر گالیله منحنی خواهد بود. اینک پدیده هایی را که برای اثبات «تساوی جرم لختی و جرم گرانشی کنش پذیر» شرح دادیم، به روشی کاملا متفاوت درک کردیم. دو گوی با هم سقوط می کنند زیرا در اصل آنها مسیرهای لخت یکسانی را در فضا-زمان دنبال می‌کنند. در نسبیت عام هیچ «نیروی گرانشی»، وجود ندارد، بدین معنی که اشتباها چنین نیرویی را به اجسام نسبت می دهیم زیرا ما هم مثل گالیله وقتی روی زمین «در حال سکون» هستیم مسیرمان شتابدار است. چارچوب مرجع متصل به سطح زمین یک چارچوب لخت نیست و «نیروی گرانشی» چارچوب به کار می رود موهوم است.

اگر این توصیف را بپذیریم، اصل هم ارزی ضعیف را برای اجسام آزاد دست می آوریم، اجسامی که «فقط» تحت تأثیر گرانش هستند در حقیقت اصلا هیچ نیرویی به آنها وارد نمی شود و بنابراین مسیر همه آنها یکسان است، اما علاوه بر اصل هم ارزی ضعیف نتیجه بارزتری نیز به دست می آوریم: اصل هم ارزی قوی. این اصل بیان می کند که نتیجه دو آزمایش که یکی در حالت «سقوط آزاد» در یک میدان گرانشی یکنواخت انجام شود و دیگری در فضایی تهی در آزمایشگاه لخت انجام شود، یکسان است. علاوه بر آن، هر آزمایشی که در یک میدان گرانشی یکنواخت «ساکن» انجام شود با آزمایشی که در فضای تهی در یک آزمایشگاه با شتاب یکنواخت انجام شود نتایج یکسان دارند. وقتی در شکل ۲۵ نیروی گرانش را حذف کنیم، می بینیم که در بالای برج به گالیله شتاب ثابتی وارد می شود، پس هر آزمایشی که او انجام می دهد باید این واقعیت را منعکس کند.
یک دلیل برای آنکه اصل هم ارزی قوی محکم تر از اصل هم ارزی ضعیف است آن است که این اصل دلالت هایی برای همه انواع آزمایش ها دارد. مثلا، یک نفر پرتو نوری را که در ابتدا مسیر افقی دارد از یک طرف آزمایشگاه متصل به زمین به طرف دیگر می فرستد. آیا پرتو نور «خم» می شود، یعنی وقتی پرتو نور به دیوار برخورد می کند انتهای آن نسبت به نقطه شروع به کف نزدیک تر می شود؟ اگر فقط اصل هم ارزی ضعیف را در نظر بگیریم، هیچ چیزی نمی توان گفت، بدین معنی که نتیجه بستگی به این دارد که نور چه چیزی باشد. اگر نور نوعی ذره با جرم لختی (و بنابراین گرانشی) باشد، پس به سمت پایین خم می شود. اگر نور نوعی پدیده موجی یا ذره ای بدون جرم باشد، سؤال همچنان باقی است.

اما اگر اصل هم ارزی قوی اعتبار داشته باشد، پرتو نور باید «به طرف پایین خم شود». برای آنکه در یک آزمایشگاه شتابدار در فضای تهی، کف آزمایشگاه «به طرف بالا شتاب می یابد»، در حالی که نور سر راه آن است پس نور در نقطه ای نزدیک تر به کف آزمایشگاه به دیوار برخورد می کند. به طور خلاصه، اصل هم ارزی قوی به سادگی خمیدگی نور در یک «میدان گرانشی» را پیش بینی می کند، صرفا به این دلیل که نور هندسه ذاتی فضا زمان را دنبال می کند. نور هرگز «خم» نمی شود؛ مسیر نور مستقیم است. در واقع، مسیر تجهیزات آزمایشگاه «ساکن » متصل به زمین خم شود. نیروهای مشهودی که از کف آزمایشگاه، میزهای آزمایش و الی اخر به تجهیزات آزمایشگاه وارد می شود، مسیر آنها را خم میکند. یکی از پیش بینی های بارز نسبیت عام – پیش بینی ای که آن را متمایز می کند از انواع نظریه های نسبیتی خاص در باب گرانش که در سال ۱۹۱۵ وجود داشت – «خمیدگی» نوری است که از کنار خورشید می‌گذرد. از زمانی که هیئت اعزامی خورشیدگرفتگی آرتور ادینگتون در سال ۱۹۱۹ این اثر را تأیید کردند، گرانش عمدتا با نسبیت عام توصیف می شود.

این ایده که فضا-زمان با تکینگی در یک سیاه چاله به پایان می رسد طبیعتا نشان می دهد که بر عکس امکان دارد فضا-زمان با یک تکینگی آغاز شده باشد. در واقع، اگر کسی از انبساط کنونی عالم به گذشته برگردد، به عالم نخستین می رسد که چگالی آن رو به افزایش است درست مثل کسی که در زمان به عقب برمی گردد. با فرض این که نسبیت عام در هر مقیاسی از انرژی برقرار باشد، نتیجه آن انفجار بزرگ، یعنی تکینگی اولیه‌ای، در تاریخ عالم است.

البته، فرض تکینگی‌های وابسته به سیاه چاله ها و انفجار بزرگ متکی به سرسپردگی راسخ به معادله میدان اینشتین است. اگر در انرژی های بالا یا خمیدگی شدید نسبیت عام نقض شود، همه شرط ها از بین می روند. علاوه بر این، در این مدل ها فرض می شود که تانسور کشش انرژی توزیع ماده و انرژی در عالم را دقیقا نمایش می دهد. معلوم نیست این فرض چگونه با روایت مکانیک کوانتومی ماده ارتباط پیدا می کند.

مسئله ادغام روایت مکانیک کوانتومی ماده با نظریه ای مثل نسبیت عام، به ویژه، مشکلی جدی است زیرا در حالی که تانسور کشش انرژی توزیع موضعی ماده و انرژی در فضا-زمان را نشان می دهد، اصلا معلوم نیست که توزیع به طور موضعی تعریف شده برای ماده با انرژی در نظریه مکانیک کوانتومی چگونه است. این امر برای درک نظریه کوانتوم مشکلات مفهومی به وجود می آورد و این به مراتب مهم تر از صرفا سازگاری نظریه کوانتوم با نسبیت است. در جلد دوم درباره این مشکلات بحث خواهیم کرد. تصور اینکه خود فضا- زمان ممکن است آغاز با پایانی داشته باشد، از نظر فلسفی کنجکاوی برانگیزترین و نیز ظریف ترین دلالت نسبیت عام است.

بسیاری از فیزیکدان ها نظریه هایی را دنبال می کنند که طبق آنها انفجار بزرگ تنها ابتدایی ترین مرحله در همسایگی محلی ما با عالم نه آغاز همه هستی است. گمانه زنی های مشابه بیان می کنند که لازم نیست سفر کاوشگر در یک تکینگی به پایان برسد، اگرچه به نظر می رسد که نیروهای جزر و مدی در هر حال سرنوشت ساز باشند. اما هر نوع نگرش دقیق به این موضوعات مستلزم فیزیک پیشرفته تری است از آنچه در حال حاضر مطرح کردیم.

 

مباحثه حفره

در فصل های ۲ و ۳ دو مبحث ارائه شده توسط لایب نیتس بر ضد فضای مطلق و زمان مطلق نیوتنی را بررسی کردیم. هر یک از این مباحثات بر اساس تقارن در فیزیک نیوتن بود. در مباحثه معروف جابه جایی استاتیک، با توجه به تقارن انتقالی و دورانی فضای اقلیدسی، استدلال می شود که برای هر توزیع محتمل ماده، توزیع حاصل از حرکت هرچیز با فاصله ثابت در یک جهت، یا دوران هر چیزی با زاویه ثابت حول یک محور، نیز یک توزیع محتمل است. اگر توزیع اولیه خودش نشان دهنده تقارن نباشد، پس توزیع جدید حالت فیزیکی محتملی از امور است که متمایز است و با همه قوانین نیوتن سازگار است. به طور مشابه جابه جایی سینماتیک سرعت های مطلق تمام ماده را به میزان ثابتی تغییر می دهد که باز هم به امکان فیزیکی متمایزی می شود. با پذیرفتن این دو امکان مدیا۔ در می رود که اصل این همانی تمیزناپدیرها و اصل جهت کافی، هر دو نقض شوند. اصل جهت کافی به این دلیل نقض می شود که خداوند برای خلق یک امکان با امکان های دیگر باید دست به انتخاب بزند. در آن فصل تذکر دادیم که اصل این همانی تمیزناپذیرها هیچ امتیاز خاصی ندارد و وارد کردن ملاحظات دینی در یک مباحثه فیزیکی جایی ندارد.

جابه جایی سینماتیک، و نه استاتیک، معلوم می کند که نیوتن پرسش های خاصی درباره واقعیت فیزیکی طرح کرده بود که نمی شد با مشاهده به آنها پاسخ داد. به ویژه، همان طور که [مثال] کشتی گالیله به روشنی نشان می دهد، بزرگی و جهت دقیق سرعت مطلق هر جزئی از ماده را نمی توان با آزمایش تعیین کرد. اما وقتی فضا و زمان مطلق نیوتن را کنار می گذاریم این مشکل در خصوص فضا-زمان گالیله‌ای با فضا-زمان نسبیتی خاص از بین می رود، زیرا دیگر هیچ سرعت مطلقی وجود ندارد که بزرگی و جهت آن برای ما معلوم نباشد.

چون جابه جایی استاتیک و سینماتیک هر دو با توسل به تقارن‌های فضا-زمان است، انتظار نمی رود که این نوع مباحث در نسبیت عام به وجود آید. فضا-زمان نسبیتی عام عمومی مطلقا چنین تقارن‌هایی ندارد. از آن جایی که خمیدگی فضا-زمان با چگالی انرژی از یک مکان به مکان دیگر تغییر می کند جواب عمومی معادله میدان اینشتین از لحاظ هندسی که همگن و نه همسان گرد است. پس جابه جایی استاتیک و سینماتیک را نمی توان تعریف کرد.

با وجود این، جان ارمان و جان نورتون مباحثه ای را مطرح کرده اند (بر اساس مجموعه ملاحظاتی بعضا متفاوت با آن چه اینشتین به روشنی بیان کرده است) که مشکل ریشه ای تری نسبیت عام را تحت تأثیر قرار می دهد. آنها این مشکل را مباحثه حفره نامیدند. برای درک این مباحثه، سه نوع تبدیلی را که در شکل ۱ نشان داده شده به خاطر بیاورید. در مباحثات جابه جایی لایب نیتس تبدیلات طول پایی به کار می روند، زیرا تحت تبدیل فاصله های نسبی و بنابراین سرعت های نسبی اجسام حفظ می شوند، در حالی که ساختار متریکی فضا- زمان پس زمینه ثابت باقی می ماند. در مباحثه حفره درست برعکس، تبدیل توپولوژیکی به کار می رود. به ویژه در این مباحثه، وابرریختی یک حفره به کار می رود، یعنی تبدیل توپولوژیکی همواری که در بیرون یک ناحیه («حفره») نگاشت همانی است اما در درون آن نگاشت همانی نیست. شکل پایین این نوع وابر ریختی حفره را نشان می دهد. در این شکل دو نمودار رسم شده است که زمینه هر دو خمینه کاملا یکسانی است، طوری که انتظار می رود موقعیت هایی که در دو نمودار با p و q و نشان داده شده اند رویدادهای کاملا یکسانی را نمایش دهند. فقط نحوه توزیع ماده و میدان ها در این رویدادها تغییر کرده است.

در نگاه اول ممکن است به نظر برسد که اگر حالت S جوابی برای معادلات میدان اینشتین باشد حالت SWARP نمی تواند جواب باشد. مثلا، می دانیم که جهان خط یک پرتو نور در خلا باید مستقیم باشد، اما به نظر می رسد پرتو نور در حالت SWARP به شدت خمیده است. ترفند وابر ریختی یک حفره این است که وقتی اشیا را مطابق با تبدیل توپولوژیکی حرکت می دهیم، نه تنها ماده و نور بلکه متریک فضا۔ زمان نین حرکت میکند. متریک فضا- زمان مانند متریک میدان الکترو مغناطیسی دست نیافتنی ربطی ندارد، بلکه این مباحثه ادعایی درباره تعین گرایی است. اگر بپذیریم که S و SWARP نشان دهنده موقعیت هایی هستند که از نظر فیزیکی محتمل اما به لحاظ هستی شناسی متفاوت اند با مشکل مواجه می شویم زیرا بیرون حفره موقعیت های فیزیکی یکسان هستند. این انتقاد به مباحثه حفره وارد است که وابر ریختی حفره سطح بیرونی آن را تغییر نمی دهد. وابرریختی یک حفره از این لحاظ به جابه جایی های لایب‌نیتس شبیه نیست، زیرا جابه جایی های لایب نیتس همیشه حالت ماده را تغییر می دهد. اما اگر S و SWARP هر دو، جواب های فیزیکی محتمل برای معادلات میدان باشند و در هر دو حالت سطح بیرونی حفره یکسان باشد، پس در اصل خود معادلات میدان باید نامتعین باشند، زیرا موقعیت فیزیکی یکدست بیرون حفره به همراه قوانین فیزیک نمی تواند موقعیت فیزیکی درون حفره را تعیین کند و چون حفره می تواند هر شکل و اندازه ای داشته باشد و پیچش می تواند شکل های نامحدود بسیاری بگیرد، این امر حاکی از عدم تعین گرایی در بالاترین حد است.

بخش عمده مباحثه حفره، آشکارا موضوع عمیقا متافیزیکی آن است بدین معنی که S و SWARP را می توان در موقعیت متافیزیکی متمایز و در عین حال در موقعیت فیزیکی محتمل تفسیر کرد. چون تفاوت های بین S و SWARP را (به جای ویژگی های کیفی مانند وجود یک جفت ذره در حال برخورد، یا یک سیاه چاله) فقط با رویدادهای نامگذاری شده منفرد می توان تعیین کرد، مبحث متافیزیکی این همانی منفردها در «جهان‌های محتمل» مختلف را باید مورد توجه قرار داد. جرمی باترفیلد (1989) یک روش پاسخ به مباحثه حفره را ارائه داده است. وی استدلال می کند که S وSWARP که صرفا نمایش های ریاضی هستند) موقعیت های متافیزیکی متمایز را نمایش نمی دهند، زیرا یک رویداد در S را تنها می توان با رویدادی در SWARP به واسطه رابطه متقابلی که دارند، مشخص کرد. اما هیچ رابطه مشابهی برای تطبیق رویداد p در S با رویدادی که نگاشت و ابرریختی p در SWARP است، وجود ندارد و برای q نیز همین طور است. پس اگر p و q در رابطه نورگونه داشته باشند، همانندهایشان در SWARP رابطه نورگونه دارند. طبق معنی شناسی دیوید لوئیس برای عبارت های صوری این بدین معنی است که اگر p و q حقیقتا رابطه نورگونه داشته باشند، هیچ جهان محتملی وجود ندارد که در آن، آنها رابطه نورگونه نداشته باشند.

اگر رویکرد سائول کریپکی به معنی شناسی صوری را بپذیریم، راه حل متفاوتی پیدا می شود. کریپکی تأکید می کند که لازم نیست موجودات جهان متقابل با رابطه های مشابه تعیین شوند: هنگام توصیف یک موقعیت می توان مستقیما به آنها تصریح کرد. پس یک نقطه خاص در SWARP رویداد واقعی P را نشان می دهد صرفا به این دلیل که من می گویم که نشان می دهد هنگامی که SWARP را بنا می کنید فرض کنید S به طرز معقولی جهان واقعی را نمایش می دهد و من در جهان واقعی دو رویداد را به ترتیب p و q مینامم. پس SWARP در واقع، رویدادهای p و q را به خلاف رابطه نورگونه شان (که در واقع نیز چنین اند) چنان نشان می دهد که رابطه فضا گونه دارند. برخلاف روش باترفیلد S و SWARP موقعیت های متمایزی را نشان می دهند. اما اصلا معلوم نیست که SWARP یک موقعیت فیزیکی با متافیزیکی محتمل را نمایش می دهد. می توانم بگوییم «اگر نیکسون یک ساندویچ ژامبون باشد…» و در پی آن تصویری به وجود آورم که طبق آن نیکسون یک ساندویچ ژامبون باشد، اما نتیجه نمی شود که به هر تعبیر احتمال دارد نیکسون یک ساندویچ ژامبون بوده باشد. علی رغم همه شرطهای زبانی من، این برخلاف ماهیت ذاتی نیکسون واقعی است که بتواند یک ساندویچ ژامبون باشد. به طور مشابه، می توانیم استدلال کنیم که اگر رویدادهای واقعی منفرد و خاص p و q رابطه نورگونه داشته باشند، آنگاه از نظر فیزیکی یا متافیزیکی این احتمال وجود ندارد که خود آن رویدادها رابطه فضاگونه داشته باشند روابط فضایی- زمانی میان رویدادهای فضا زمان برای همانندی آنها ضروری است. برای جوابگویی به این روش به (1989) Maudlin مراجعه کنید.

راه حل سوم را کارل هوفر و نانسی کارت رایت (1994) پیشنهاد دادند. این راه حل عدم تعین بنیادی را که ارمان و نورتن پیشنهاد می دهند تصدیق می کند اما اصرار می ورزند که این عدم تعین بی ضرر است و نگران کننده نیست. اگر S و SWARP موقعیت های فیزیکی محتمل متفاوتی باشند، به هر مخلوقی که در آنها به وجود بیاید دقیقا به یکسان نگاه و آن را احساس می کنند. هیچ آزمایشی را نمی توان توصیف کرد که پیامد مشاهده پذیر آن در S و SWARP متفاوت باشد. مانند وقتی که در جابه جایی استاتیک به هیچ پرسش روشنی درباره جهان واقعی نمی توان پاسخ داد زیرا از لحاظ تجربی دست نیافتنی است. ارمان و نورتن فکر می کنند که عدم تعین را، حتی اگر هیچ پیامد تجربی ای نداشته باشد، چون از هیچ منبع فیزیکی معقول به دست نیامده است، هنوز نمی توان پذیرفت. آنها می گویند که تعین گرایی ممکن است درست نباشد، اما حداقل باید شانس جنگیدن داشته باشد. در واقع، باید معلوم شود که شکل اصلی مباحثه حفره در فضا- زمان گالیله ای و نیوتنی هم به اندازه نسبیت عام کاربرد دارد، زیرا اگر رویدادهای فضا-زمان به طور تصادف فقط ساختار هندسی داشته باشند، پس طرح حفره در هر فضا کارآمد خواهد بود.

پس چندین روش برای پاسخ به مباحثه حفره وجود دارد. این مباحثه هنوز هم ممکن است الهام بخش روایت متافیزیکی کاملا جدیدی از فضا و زمان باشد، روایتی که از مباحثه حفره به این شکل در امان است. تا امروز، هیچ جایگزینی برای آن یافت نشده است. فقط گذر زمان این امر را روشن می کند.

 

به‌زودی تکمیل خواهد شد…